Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Regra de 1/3 de Simpson

Ver Todos os Exercícios

Teoria

Fala aí! Seja muito bem vindo ao Responde Aí! Bora aprender sobre o Método de 1/3 de Simpson?

Você já deve conhecer os métodos de integração de cálculo, mas imagina que você tenha que integrar essa função aqui:

Putz, que sufoco! 😱

Mas é pra isso que existe as Integrações Numéricas! Aqui a gente vai usar artifícios do cálculo numérico para resolver integrais que seriam bem trabalhosas de resolver analiticamente! 😍

No vídeo abaixo tem um resumão de TUDO que você precisa saber pra começar usar a Regra de 1/3 de Simpson para resolver integrais cabulosas! 👇

Ou continua comigo no textinho!

Fórmula de Simpson

Indo bem direto ao ponto, a fórmula que vamos usar na Regra de 1/3 de Simpson é essa daqui:

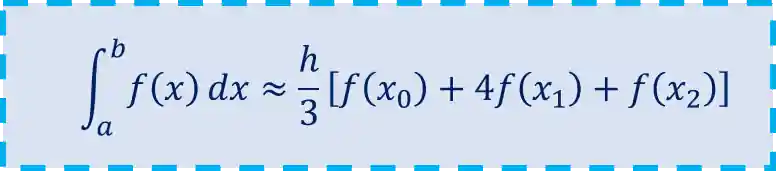
Regra 1/3 de Simpson: Fórmula
Regra 1/3 de Simpson: Fórmula

Mas calma, não se desespera que vamos entender tudinho passo a passo!

Na Regra de 1/3 de Simpson usamos um polinômio interpolador de Lagrange de ordem para aproximar a função de interesse .

-Que?

Se liga na imagem abaixo que tudo vai ficar mais claro:

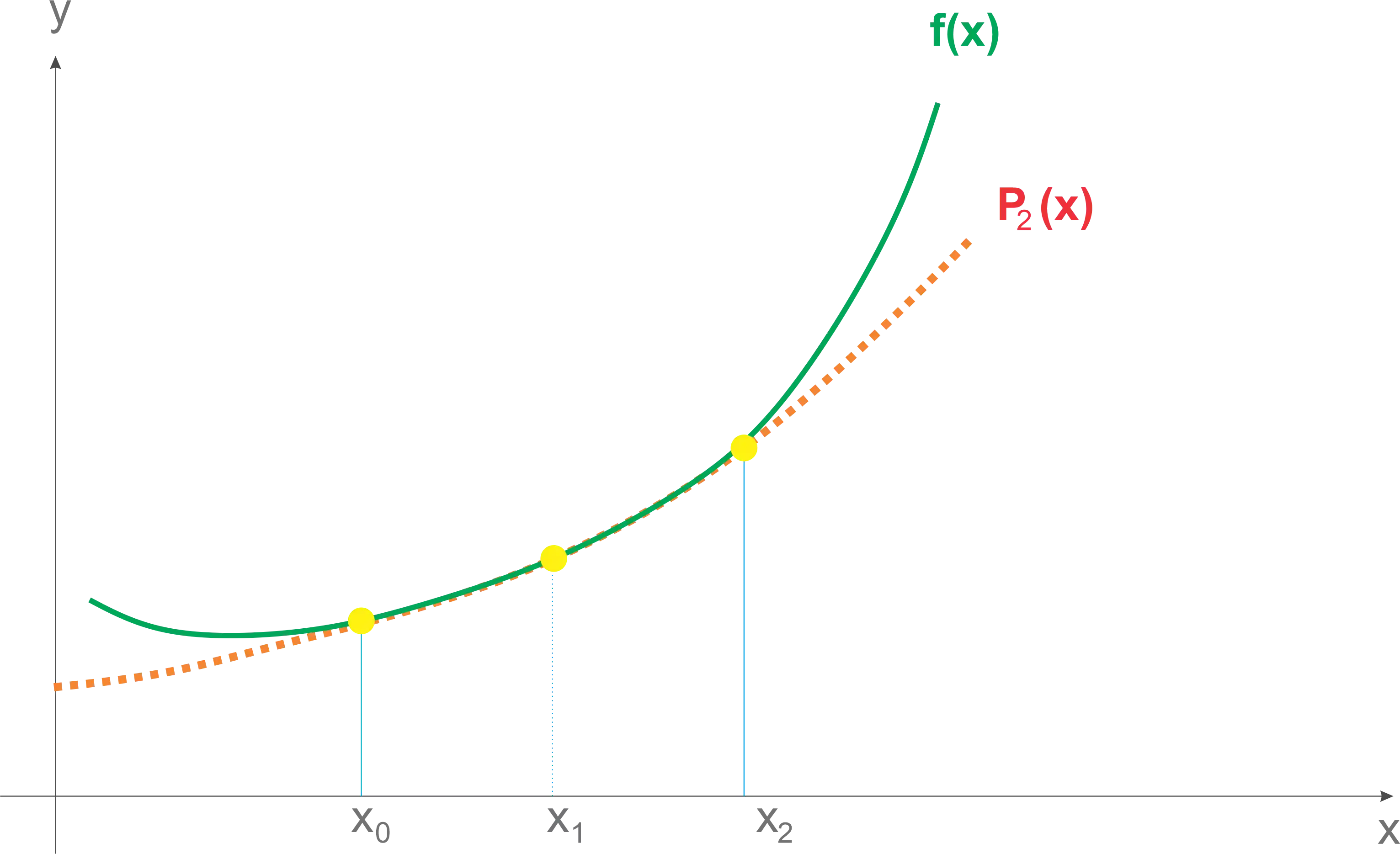
Regra 1/3 de Simpson: Exemplo Gráfico
Regra 1/3 de Simpson: Exemplo Gráfico

Supondo que é a nossa função de interesse e queremos saber a área sob a curva entre os pontos e , ou seja, queremos integrar a função nesse intervalo!

Para isso usamos um polinômio de grau , que vai se ajustar ao nesse intervalo e assim conseguimos fazer a integração! vai ter essa carinha aqui:

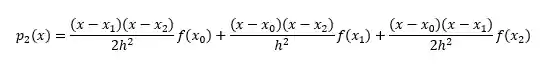
Polinômio Interpolador de grau 2.
Polinômio Interpolador de grau 2.

O nosso intervalo fica entre e , mas precisamos de pontos para o nosso polinômio, então vamos usar o ponto intermediário . Esses pontos devem ser igualmente espaçados e o espaço entre esses pontos vai se chamar .

Integrando e fazendo umas manipulações, chegamos nessa fórmula pra definir a regra de 1/3 de Simpson:

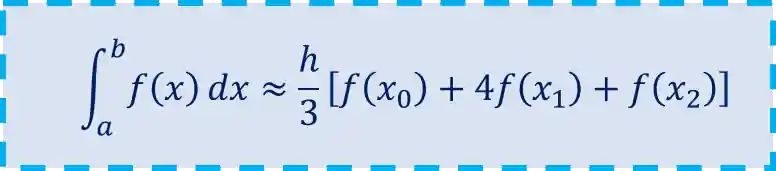
Regra 1/3 de Simpson: Fórmula
Regra 1/3 de Simpson: Fórmula

Que é essa daqui que a gente viu lá em cima! 😍

Um raciocínio bem parecido é usado na Regra dos Trapézios, mas a Regra de 1/3 de Simpson é considerada melhor que a Regra dos Trapézios, pois apresenta um erro menor em seus resultados, apesar de ser mais trabalhosa!

Falando em erro, o erro da Fórmula de Simpson é dado por:

Como usar a Regra de 1/3 de Simpson?

Vamos aprender fazendo um exemplo?!

A beleza desse exemplo é que essa integral é muito fácil de fazer analiticamente! Então podemos fazer das duas formas e comparar os resultados!

Vamos usar os seguintes pontos:

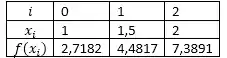
Tabela de dados.
Tabela de dados.

Usaremos a fórmula:

Para calcular fazemos:

Agora é só substituir e calcular:

Analiticamente, teríamos:

Suuuper próximo, viu?!

Mas nem sempre podemos comparar com o resultado analítico, nesse caso calculamos o erro:

E agora, se eu te contar que da pra fazer esse método ficar ainda mais preciso?

Regra 1/3 de Simpson Repetida

Uma coisa bem importante é que nesse método aproximamos a função usando parábolas! Isso significa que precisamos de pontos consecutivos pra traçar a parábola.

E se, em cada par de intervalos vamos aplicar a regra individual que vimos lá em cima. Com .

No final vamos chegar na aproximação:

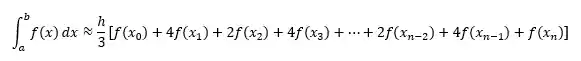
Regra 1/3 de Simpson Repetida
Regra 1/3 de Simpson Repetida

Organizando os termos:

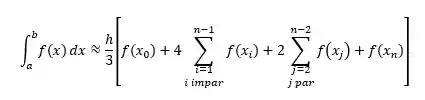
Regra 1/3 de Simpson Repetida - Fórmula simplificada
Regra 1/3 de Simpson Repetida - Fórmula simplificada

Assim teremos mais pontos e consequentemente uma precisão maior!

Algoritmo

Esse algoritmo é para a Regra 1/3 de Simpson Repetida. Para que ela vire a Regra 1/3 de Simpson normal basta você dar pontos para ela. Lembrando que para termos um número par de intervalos precisamos de um número ímpar de pontos.

  • Passo 1: Dados iniciais (o que seu programa vai receber de você):
    • Vetor de valores
    • Vetor de valores

  • Passo 2. Definimos

  • Passo 3. Definimos

  • Passo 4: Para de a repita o passo .

  • Passo 5: Se for par faça o passo Se for ímpar, faça o passo .

  • Passo 6:

  • Passo 7:

  • Passo 8:

  • Passo 9: Retorne

Novamente, poderíamos adaptar esse código para entrarmos com os extremos e com o número de intervalos ao invés dos valores de . Uma condição interessante de se adicionar é verificarmos se é par no começo das iterações !

Pra fechar com chave de ouro, confere esse exercício resolvido em vídeo sobre a Regra de 1/3 de Simpson:


Agora vamos fazer uns exercícios!

Como usar a Regra de 1/3 de Simpson?

Regra 1/3 de Simpson Repetida

Algoritmo

Exercícios Resolvidos

Exercício Resolvido #1

Lista 5 – Professor Mauro – UFRJ – Questão 5

Dê um exemplo de uma função onde a regra 1/3 de Simpson calcula o valor exato da integral.

Passo 1

Como vimos na teoria, qualquer integral de uma função de grau igual ou menor que três tem o erro zerado quando usamos esse método.

Resposta

Qualquer polinômio de grau ≤ 3 .

Exercício Resolvido #2

Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 305, exemplo 2

Seja I = ∫ 0 1 e x d x .

a Calcule uma aproximação para I usando a regra 1/3 de Simpson com n = 10 . Estime o erro cometido.

b Para que valor de n teríamos erro inferior a 10 - 3 ?

Passo 1

a Como n = 10 , temos h = 1 10 = 0.1 . Fazendo a tabelinha:

Jogando na fórmula:

I ≈ 0.1 3 f x 0 + 4 f x 1 + f x 3 + … + f x 9 + 2 f x 2 + f x 4 + … + f x 8 + f x 10

I ≈ 0.1 3 1 + 4 8.578 + 2 6.761 + 2.718

I ≈ 1.7184

Passo 2

Para estimar o erro cometido usamos a fórmula:

E ≤ n h 5 180 ∙ max x ∈ a , b ⁡ f i v x

A derivada quarta de e x é o próprio e x , e ele tem valor máximo no intervalo 0,1 em x = 1 , onde temos f i v 1 = 2.718 . Além disso, sabemos que n = 10 e que h = 0.1 . Logo:

E ≤ 10 0.1 5 180 ∙ 2.718

E ≤ 1.51 × 10 - 6

É importante ressaltarmos que trabalhamos com apenas três casas decimais nas contas então nossa aproximação de I certamente não tem o erro que estimamos! Esse limitante do erro considera que fizemos as contas com todas as casas decimais possíveis.

Passo 3

b Repare que usando n = 10 obtivemos um erro da ordem de 10 - 6 ! Isso quer dizer que para termos um erro menor que 10 - 3 podemos diminuir bastante esses intervalos!

Sabemos que h = b - a n . Logo, nossa fórmula do erro pode ser reescrita como:

E ≤ b - a 5 180 n 4 ∙ max x ∈ a , b ⁡ f i v x

Substituindo os valores que já temos: 1 5 180 n 4 ∙ 2.718 ≤ 10 - 3

n 4 ≥ 15.1

n ≥ 1.97

Como n deve ser par e inteiro, temos que:

n ≥ 2

Resposta

a I ≈ 1.7184

E ≤ 1.51 × 10 - 6

b n ≥ 2

Exercício Resolvido #3

Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 314, exercício 15

Usando a regra de Simpson, calcule o valor de ∫ 1 2 d x x com precisão de 4 casas decimais. Compare o resultado com o valor de ln ⁡ 2 .

Passo 1

Primeiro temos que encontrar o número mínimo de intervalos que nos garante uma precisão de 4 casas decimais, ou seja, 10 - 4 . Então:

n h 5 180 ∙ max x ∈ a , b ⁡ f i v x ≤ 10 - 4

A derivada quarta de f x é dada por:

f x = 1 x

f ' x = - 1 x 2

f ' ' x = 2 x 3

f 3 x = - 6 x 4

f 4 x = 24 x 5

E o valor máximo do módulo dessa derivada no intervalo 1,2 acontece em x = 1 , onde temos f 4 1 = 24 .

Por fim, usando a relação h = b - a n temos:

1 5 180 n 4 ∙ 24 ≤ 10 - 4

n 4 ≥ 1333.333

n ≥ 6.043

E como n deve ser inteiro e par,

n ≥ 8

Passo 2

Agora vamos aproximar a integral usando 8 intervalos, ou seja, h = 1 8 = 0.125 . A tabela fica:

∫ 1 2 d x x ≈ 0.125 3 1 + 4 2.7649 + 2 2.0381 + 0.5

∫ 1 2 d x x ≈ 0.69316

O resultado exato seria ln ⁡ 2 = 0.69314718 . Ou seja, o erro foi de:

E = 0.69316 - 0.69314718 = 0.1282 × 10 - 4

Que é menor que 10 - 4 como esperávamos.

Resposta

∫ 1 2 d x x ≈ 0.69316

ln ⁡ 2 = 0.69314718

E = 0.69316 - 0.69314718 = 0.1282 × 10 - 4

Exercício Resolvido #4

Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 312, exercício 7

Use a regra 1/3 de Simpson para integrar a função abaixo entre 0 e 2 com o menor esforço computacional possível (menor número de divisões e maior precisão). Justifique. Trabalhe com três casas decimais.

f x = x 2 ,       s e   0 ≤ x ≤ 1 x + 2 3 ,       s e   1 < x ≤ 2

Passo 1

Você tem que se lembrar do seguinte: a regra 1/3 de Simpson aproxima integrais sem erro nenhum de polinômios de grau menor ou igual a 3 !

E como nossa função é subdividida em polinômios de grau 2 e 3 , usando o número mínimo de divisões necessárias para aplicarmos a regra já estamos garantindo a precisão máxima.

Sendo assim, precisamos dividir essa função em 4 intervalos. Dois intervalos para aproximarmos o polinômio x 2 e dois para aproximarmos o x + 2 3 !

Passo 2

Montando a tabela desse problema vamos ter:

Observe que como no ponto 1 temos uma descontinuidade, usei os limites laterais para que a conta desse certinha! Se não usássemos esse artifício nosso resultado final certamente não seria sem erro nenhum!

Na prática o que estamos fazendo é dividindo nossa integral dessa forma:

∫ 0 2 f x d x = ∫ 0 1 x 2 d x + ∫ 1 2 x + 2 3 d x

E resolvemos cada uma dessas integrais pela regra 1/3 de Simpson:

∫ 0 2 f x d x = 0.5 3 0 + 4 0.25 + 1 + 0.5 3 27 + 4 42.875 + 64 = 44.083

Resposta

Obtemos o menor esforço computacional com 4 intervalos e erro igual a 0 .

∫ 0 2 f x d x = 44.083

Exercício Resolvido #5

Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 312, exercício 6

Determinar h , a distância entre x i e x i + 1 , para que se possa avaliar ∫ 0 π / 2   cos ⁡ x d x com erro inferior a ε = 10 - 3 pela regra de Simpson.

Passo 1

O limitante para o erro pela regra 1/3 de Simpson é dado por:

E ≤ n h 5 180 ∙ max x ∈ a , b ⁡ f i v x

Calculando a derivada de ordem 4 :

f x = cos ⁡ x

f ' x = - sin ⁡ x

f ' ' x = - cos ⁡ x

f 3 x = sin ⁡ x

f 4 x = cos ⁡ x

E o valor de maior módulo que cos ⁡ x assume no intervalo 0 , π 2 é 1 . Por último substituímos n = b - a h . Sendo assim, temos:

E ≤ n h 5 180 ∙ max x ∈ a , b ⁡ f i v x

E ≤ b - a h 4 180 ∙ 1 ≤ 10 - 3

h 4 ≤ 0.11459

h ≤ 0.581819

Passo 2

Ué, passo 2 por quê? Não acabou não?

Não! A gente quase se esquece de um detalhe importantíssimo! O nosso n tem que ser inteiro e par! O n nesse caso vale:

n = b - a h = π 2 0.581819 = 2.7

Então, h ≤ 0.581819 implica em n ≥ 2.7 . E o próximo número par inteiro maior que 2.7 é 4 . Logo,

h ≤ b - a n = π 2 4 = π 8

E esse é o nosso h ! Pegadinha safada essa né?

Resposta

h ≤ π 8

Exercício Resolvido #6

Lista de Exercícios - FEI

Determinar o menor número de pontos necessários para calcular a integral ∫ 0 π 3 cos ⁡ x d x pela regra de simpson com erro inferior a 0,001

Passo 1

Fala pessoinha, se você deu uma olhada no nosso conteúdo de método do trapézio, você viu esse exercício lá. Agora vamos ver que pelo método de simpson vai precisar de bem menos pontos para o mesmo erro

Nesses casos onde o professor pergunta pra gente qual o número de pontos necessário, a gente vai se apegar com força na fórmula do limitante de erro, que é essa aqui oh:

E ≤ n h 5 180 *   max x ∈ [ a , b ] ⁡ f i v ( x )

Com ela a gente vai conseguir calcular o passo que é o “h” e já já te mosto como o h leva a gente até o número de pontos.

Essa parte mais a direita da fórmula meio estranha só quer dizer que eu preciso achar o máximo valor do módulo da derivada quarta no intervalo onde eu estou integrando..então bora derivar! Essa é mole...

f ' x = - s e n x

f ' ' x = - c o s ⁡ ( x )

f ' ' ' x = s e n ( x )

f i v x = c o s ⁡ ( x )

No nosso intervalo de integração, o valor de x que faz | f i v x | ser máximo é x=0 . Nesse caso a fórmula do erro ficaria:

E ≤ n h 5 180

Se o erro é sempre menor ou igual a n h 5 180 e queremos limitar ele à 0.001, Então podemos escrever: n h 5 180 < 0.001  

Passo 2

Bom ta na hora de usar aquela sacada que o professor acha que vc não manja. Podemos escrever h desse jeito aqui:

h = b - a n

O b e o a são os extremos superior e inferior da integral e n o número de intervalos. E veja só

k = n + 1

O número de pontos necessários k é o número de intervalos mais um, viu só como o h salvou nossa vida!!! Nesse exercício o intervalo de integração é [ 0 ,   π / 3 ] então...

h = π 3 n

Passo 3

Substituindo na nossa inequação:

n ( π 3 n ) 5 180 < 0.001

Resolvendo ficamos com...

1 n 4 < 0.001 * 180 * 3 5 π 5

Invertendo de ambos os lados n 4 > 6.9963

Elevando a 1 4 ambos os lados

n > 1.62

Passo 4

Com n deve ser um número inteiro, sempre vamos arredondá-lo para cima, nesse caso n = 2

Como a pergunta foi o número de pontos e não de intervalos (pegadinha do professor), é só somar 1 ao número de intervalos n .

LEMBRETE: Para usar a regra de simpson k deve sempre ser ímpar. Portanto se encontrassemos k=4, arredondaríamos para o número ímpar imediatamente superior k=5.

Resposta

k = 3 pontos. (Bem menos que usando regra do trapézio )

Exercício Resolvido #7

Lista de Exercícios – FEI (Adaptado)

Uma criança rolando uma pedra x metros utiliza uma força de 𝑓(𝑥) = 15 + 3𝑠𝑒𝑛(𝑥) dada em Newtons. Sabe-se que o trabalho realizado pela criança para rolar π / 2 metros é dado por W = ∫ 0 π / 2 f ( x ) d x . Determine o número de integrais usando pela fórmula de Simpson com erro de truncamento menor que 0.0004.

Passo 1

Pega essa criança possuída pelo demônio que consegue fazer uma força senoidaaaal!!! Dito isso, fico mais tranquilo pra te dizer que sempre que o professor pedir número de intervalos, pontos ou integrais, vamos sempre nos apegar a fórmula do limitante de erro, que é essa aqui:

E ≤ n h 5 180 *   max x ∈ [ a , b ] ⁡ f i v ( x )

Mas nesse caso podemos reescrever ela assim oh:

E ≤ n 2 * h 5 90 *   max x ∈ [ a , b ] ⁡ f i v ( x )

E esse n 2 vai ser o número de integrais de simpson utilizadas. Basta encontrarmos n agora né?!

Passo 2

Essa parte mais à direita da fórmula meio estranha só quer dizer que eu preciso achar o máximo valor do módulo da derivada quarta no intervalo onde eu estou integrando... Então bora derivar!

f ' x = 3 c o s x

f ' ' x = - 3 s e n ⁡ ( x )

f ' ' ' x = - 3 c o s ( x )

f i v x = 3 s e n ( x )

No nosso intervalo de integração, o valor de x que faz | f i v x | ser máximo é x = π 2 . Nesse caso a fórmula do erro ficaria:

E ≤ 3 n h 5 180

Se o erro é sempre menor ou igual a 3 n h 5 180 e queremos limitar ele à 0.0004, então podemos escrever: 3 n h 5 180 < 0.0004  

Passo 3

Bom ta na hora de usar aquela sacada que o professor acha que vc não manja. Podemos escrever h desse jeito aqui:

h = b - a n

O b e o a são os extremos superior e inferior da integral e n o número de intervalos. Nesse exercício o intervalo de integração é [ 0 , π 2 ] então...

h = π 2 n

Passo 4

Substituindo na nossa inequação:

3 n ( π 2 n ) 5 180 < 0.0004

Resolvendo ficamos com...

1 n 4 < 0.0004 * 180 * 2 5 3 π 5

Invertendo de ambos os lados n 4 > 398,46313

Elevando a 1 4 ambos os lados

n > 4,47

Passo 5

Com n deve ser um número inteiro, sempre vamos arredondá-lo para cima, nesse caso n = 5

Como a pergunta foi o número de integrais de simpson e não de intervalos (pegadinha do professor), é só dividir n por 2.

n 2 = 2 , 5

Ou seja, no mínimo, 3 integrais de simpson são suficientes.

Resposta

3 integrais de Simpson

Exercício Resolvido #8

Lista de Exercícios - FEI

Calcular a área aproximada limitada por 𝑦 = 𝑙𝑛(𝑥 + 1), 𝑥 = 2, 𝑥 = 3 e 𝑦 = 0, utilizando a fórmula de simpson com o menor número de pontos e erro E < 0.0 1 .

Passo 1

Bom, a primeira coisa que a gente precisa fazer é achar o número intervalos n que precisamos usar pra resolver com esse erro que o professor determinou, pra isso é só usar a fórmula do limitante de erro.

E ≤ n h 5 180 *   max x ∈ [ a , b ] ⁡ f i v ( x )

Passo 2

Essa parte mais a direita da fórmula meio estranha só quer dizer que eu preciso achar o máximo valor do módulo da derivada quarta no intervalo onde eu estou integrando..então bora derivar!

f ' x = 1 x + 1

f ' ' x = - 1 x + 1 2

f ' ' ' x = 2 x + 1 3

f i v x = - 6 x + 1 4

No nosso intervalo de integração, o valor de x que faz | f i v x | ser máximo é x = 2 . Nesse caso a fórmula do erro ficaria:

E ≤ 2 n h 5 180 * 27

Lembre que na fórmula do erro usamos o módulo da f i v ( x ) por isso que a gente esquece o sinal.

Se o erro é sempre menor ou igual a 2 n h 5 180 * 27 e queremos limitar ele à 0.01, Então podemos escrever: 2 n h 5 180 * 27 < 0.01  

Passo 3

Bom ta na hora de usar aquela sacada que o professor acha que vc não manja. Podemos escrever h desse jeito aqui:

h = b - a n

O b e o a são os extremos superior e inferior da integral e n o número de intervalos. Nesse exercício o intervalo de integração é [ 2,3 ] então...

h = 1 n

Passo 4

Substituindo na nossa inequação a equação do h :

2 n ( 1 n ) 5 180 * 27 < 0.01

Resolvendo ficamos com...

1 n 4 < 0.01 * 180 * 27 2

Invertendo de ambos os lados n 4 > 0.0412

Elevando a 1 4 ambos os lados

n > 0.4504

Passo 5

Com n deve ser um número inteiro, sempre vamos arredondá-lo para cima, nesse caso n = 1 , o que resultaria em k=2 ponto. Maaaaas em Simpson o número mínimo de pontos para fazer mos a integral são 3... então bora tabelar a nossa função usando 3 pontos.

Passo 6

Como agora a gente já sabe que vai usar uma tabela com k=3 pontos, já dá pra calcular o passo h da nossa tabela de x pela f ( x ) .

n = k - 1

n = 2

h = 1 n

h = 0.5

Logo nossa tabela andará de 0.5 em 0.5.

Passo 7

Nossa tabela ficou assim:

Substituindo na f ( x ) os valores de x da nossa tabela teremos:

Agora é só aplicar a fórmula de simpson.

Passo 8

Olha lá a fórmulinha para 3 pontos:

∫ 2 3 l n ⁡ ( x + 1 ) d x ≈   h 3 f ( x 0 ) + 4 f ( x 1 ) + f ( x 2 ) ]

Passo 9

∫ 2 3 l n ⁡ ( x + 1 ) d x ≈   0.5 3 [ 1.0986 + 4 * 1.2528 + 1.3863 ]

Resolvendo a continha do lado direito

∫ 2 3 l n ⁡ ( x + 1 ) d x ≈   1.2493

Resposta

∫ 2 3 l n ⁡ ( x + 1 ) d x ≈   1.2493

Exercícios de Livros Relacionados

Determine, com precisão de duas casas decimais, as áreas das superfícies geradas pela rotação da curva ao longo do eixo x y =s e nx, x ∈ 0 , π
Sua empresa de fabricação de metal está tentando fechar contrato para produzir folhas onduladas de metal para telhado, como mostramos a seguir. As seções transversais dessas folhas devem se ajustar à
Calcule a integral definida por dois métodos: a ) use a fórmula prismoidal dada no exercício 44 ; b ) use o segundo teorema fundamental do Cálculo ∫ - 2 2 x 3 + x 2 - 4 x - 2 d x
A forma de um estacionamento é irregular e o comprimento do terredo de oeste a leste é 240m . No extremo oeste do terreno a largura é de 150m e no extremo leste é de 175m . Em 40,80,120,160 e 200m do
Mostre que o valor exato da integral abaixo é igual a π , interpretando como medida da área de uma região. Use a regra de simpsom para n=6 e prove por aproximação que o valor da integral é π . ∫ 0 1 4