Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Quadratura Gaussiana

Ver Todos os Exercícios

Teoria

Quadratura Gaussiana é um método de integração numérica bastante útil quando a gente tem integrais muito complicadas pra resolver pelo método analítico! O método analítico é a forma tradicionalzona de calcular integrais, que a gente aprende lá no cálculo!

Bora aprender como o Método da Quadratura Gaussiana funciona?!

📢 Clique para ver mais:

Como Calcular a Integral Gaussiana

O método da Quadratura Gaussiana escolhe pontos para otimizar a aproximação da integral ao invés de simplesmente escolher alguns pontos igualmente espaçados!

-Mas como?! 😖

Vamos começar pelo mais simples, vou te mostrar como funciona para a integral de uma função no intervalo usando pontos e depois a gente vai para os casos genéricos, beleza?!


Nós vamos aproximar a integral usando a seguinte fórmula:

Essa aproximação vai nos dar o valor exato da integral para polinômios de grau menor ou igual a . Nesse caso, onde , a aproximação não deve ter erro para polinômios de grau menor ou igual a . Então vamos encontrar essas funções que podem ser aproximadas sem erro, ou seja:

Substituindo cada uma delas na aproximação:

Com isso chegamos a um sistema de variáveis:

Resolvendo esse sistema chegamos em:

O que nos dá a fórmula de aproximação:

Prontinho!! Você também pode conferir esse conteúdo em vídeo:

Quadratura Gaussiana com n maiores que 2

Nós vimos como fica a aproximação para . Para maiores faríamos o mesmo passo a passo.
A diferença é que a cada que acrescentamos aparecem novas variáveis e novas equações. Mas, por outro lado, a cada que acrescentamos, diminuímos o erro do método também, já que vimos que esse método dá o valor exato para polinômios de grau ou menor.

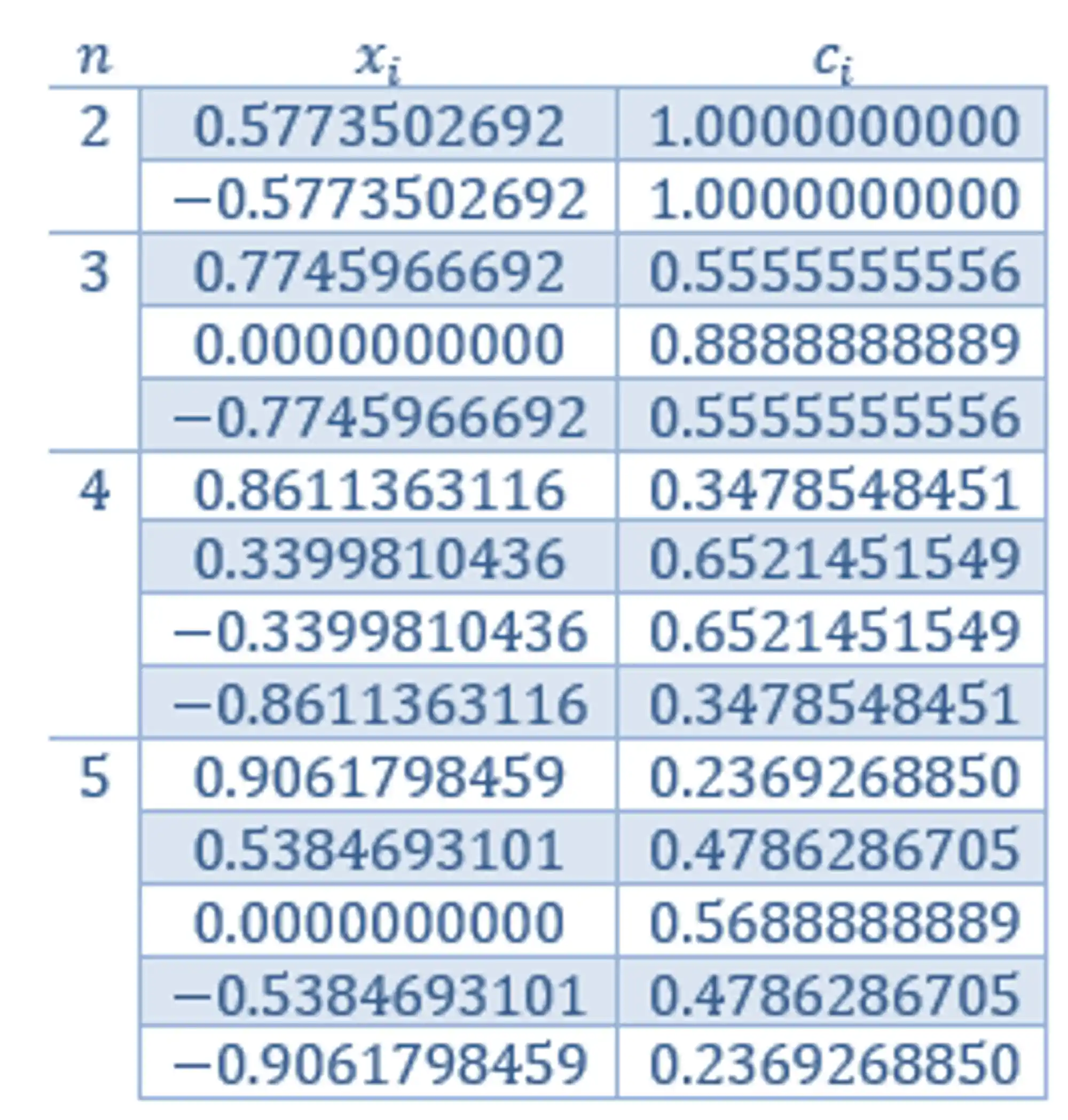
A boa notícia é os valores das constantes e para cada são tabelados. Se liga só:

Quadratura Gaussiana com n maiores que 2
Quadratura Gaussiana com n maiores que 2

Quadratura Gaussiana com Intervalos Genéricos de Integração

Imagina que você não quer mais integrar no mas quer integrar em um qualquer. Nesse caso é só aplicarmos uma mudança de variáveis, que vai servir para termos um novo intervalo. Assim:

Assim, temos:

Ou seja, trocamos um que ia de para por um que vai de a !

Algoritmo da Integral Gaussiana

O problema do método da quadratura gaussiana é a necessidade de utilizar a função f(x) que muda com o problema. Sendo assim, antes de usá-lo é necessário definir essa função separadamente! Além disso o seu algoritmo deve definir as constantes e a serem usadas para cada . O algoritmo que eu vou apresentar aqui terá apenas os valores tabelados de e mas você pode adicionar os outros.

Agora vamos para o passo a passo do algoritmo da quadratura gaussiana!

Passo 1: Inserir os dados iniciais do programa

A primeira coisa que devemos fazer aqui é inserir os dados iniciais, que são:

  • Número de pontos,
  • Intervalo,

Passo 2: Se n=2, vá para o passo 3. Se n=3, vá para o passo 4.

Aqui não tem mistério, é só analisar o número de pontos! Se ele for igual a 2 a fórmula utilizada esta no passo 3 e se for igual a 2, usaremos a fórmula do passo 4.

Passo 3: Se n=2, então retornamos o valor:

Caso o número de pontos seja igual a 2, usamos a seguinte fórmula:

Passo 4: Se n=3, então retornamos o valor:

Se o número de pontos for igual a 3, usamos:

Agora vamos praticar com exercícios?

Quadratura Gaussiana com Intervalos Genéricos de Integração

Algoritmo da Integral Gaussiana

Exercícios Resolvidos

Exercício Resolvido #1

Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 314, exercício 12

Deduza a fórmula de integração da forma

∫ - 1 1 f x d x ≈ w 0 f - 0.5 + w 1 f 0 + w 2 f 0.5

que integre exatamente polinômios de grau ≤ 2 .

Passo 1

Então pra resolver isso vamos usar a mesma lógica lá da teoria quando deduzimos a fórmula da quadratura gaussiana de dois pontos. Como a fórmula deve integrar exatamente polinômios de grau ≤ 2 , então nossa aproximação passa a ser uma igualdade nesses casos:

f x = 1

f x = x

f x = x 2

Onde temos:

w 0 ∙ 1 + w 1 ∙ 1 + w 2 ∙ 1 = ∫ - 1 1 1 d x = 2

w 0 - 0.5 + w 2 0.5 = ∫ - 1 1 x d x = 0

w 0 0.25 + w 2 0.25 = ∫ - 1 1 x 2 d x = 2 3

Passo 2

Chegamos então no sistema:

w 0 + w 1 + w 2 = 2 - 0.5 w 0 + 0.5 w 2 = 0 0.25 w 0 + 0.25 w 2 = 2 3

Da segunda equação temos que:

w 0 = w 2

Substituindo isso na terceira equação:

0.5 w 0 = 2 3

w 0 = w 2 = 4 3

Substituindo na primeira equação:

8 3 + w 1 = 2

w 1 = - 2 3

Logo, nossa fórmula de integração fica:

∫ - 1 1 f x d x ≈ 4 3 f - 0.5 - 2 3 f 0 + 4 3 f 0.5

Resposta

∫ - 1 1 f x d x ≈ 4 3 f - 0.5 - 2 3 f 0 + 4 3 f 0.5

Exercício Resolvido #2

Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 315, exercício 17 adaptado

Considere a integral:

I = ∫ 0 1 e - x 2 d x

a Estime I por Quadratura Gaussiana com 2 pontos.

b Sabendo que o valor exato de I (usando 5 casas decimais) é 0.74682 , compare a estimativa dada.

c Quantos pontos seriam necessários para que a regra dos Trapézios e 1/3 de Simpson obtivessem essa mesma precisão?

Passo 1

a Essa primeira letra não tem mistério nenhum né? Só temos que tomar cuidado que os limites da integral são 0,1 e não - 1,1 ! Então temos que lembrar da fórmula da mudança de intervalos de integração:

x = 1 2 b - a t + a + b  

d x = b - a 2 d t

Logo,

I = ∫ 0 1 e - x 2 d x = 1 2 ∫ - 1 1 exp ⁡ - t + 1 2 2 d t ≈ 1 2 exp ⁡ - - 3 3 + 1 2 2 + exp ⁡ - 3 3 + 1 2 2

I ≈ 0.74659

Passo 2

b Sabendo que o valor exato com 5 casas decimais é 0.74682 podemos encontrar o erro:

E A = 0.74659 - 0.74682 = 0.00023

Passo 3

c Lembram-se das fórmulas do limitante do erro para as regras do Trapézio e 1/3 de Simpson repetidas? Não? Bom, eu não lembro delas então não se sintam mal haha. São essas aqui oh:

Trapézios Repetida:

E ≤ n h 3 12 ∙ max x ∈ a , b ⁡ f ' ' x

1/3 de Simpson Repetida:

E ≤ n h 5 180 ∙ max x ∈ a , b ⁡ f i v x

Agora vamos achar qual o n necessário em cada caso. Lembrando que h = b - a n = 1 - 0 n !

Passo 4

Para a regra dos trapézios temos:

1 3 12 n 2 ∙ max x ∈ a , b ⁡ f ' ' x ≤ 0.00023

Temos que:

f x = e - x 2

f ' x = - 2 x e - x 2

f ' ' x = e - x 2 4 x 2 - 2

E o máximo de f ' ' x em 0,1 acontece em x = 0 onde temos f ' ' x = 2 . Substituindo na fórmula:

1 3 12 n 2 ∙ 2 ≤ 0.00023

n 2 ≥ 724,64

n ≥ 26,91

Logo, temos n ≥ 2 7 intervalos! O que nos diz que precisaríamos de pelo menos 2 8 pontos! Muito cuidado com essa relação intervalo-pontos haha. Como a questão pede o número de pontos você tem que somar 1 no número de intervalos!

Passo 5

Para a regra 1/3 de Simpson temos: 1 5 180 n 4 ∙ max x ∈ a , b ⁡ f i v x ≤ 0.00023  

Continuando as derivadas:

f 3 x = - 4 x 2 x 2 - 3 e - x 2

f 4 x = 4 4 x 4 - 12 x 2 + 3 e - x 2

E o máximo de f 4 x no intervalo 0,1 ocorre em x = 0 e tem como valor f 4 x = 12 . Substituindo:

1 5 180 n 4 ∙ 12 ≤ 0.00023

n 4 ≥ 289.86

n ≥ 4.13

Nesse caso como precisamos de um número par de intervalos nossa condição fica n ≥ 6 . Ou seja, precisamos de 7 pontos.

Resposta

a I ≈ 0.74659

b E A = 0.00023

c 2 8 pontos para a regra dos Trapézios e 7 pontos para a regra 1/3 de Simpson.

Exercício Resolvido #3

Lista 8 – UNICAMP – Exercício 11

Calcule as integrais abaixo usando Quadratura Gaussiana. Utilize 5 casas decimais.

a ∫ 1 4 x d x , com 2 pontos.

b ∫ 0 1 sin ⁡ x x d x , com 3 pontos.

Passo 1

a Aqui é só aplicar a fórmula lembrando de fazer a mudança de intervalo de integração:

x = 1 2 3 t + 4 + 1 = 3 t + 5 2

d x = 3 2 d t

∫ 1 4 x d x = 3 2 ∫ - 1 1 3 t + 5 2 d t ≈ 3 2 3 - 3 3 + 5 2 + 3 3 3 + 5 2 = 4.66941

Passo 2

b Lembrando que para 3 pontos temos o seguinte:

x 0 = 0.77460

c 0 = 0.55556

x 1 = 0.0000

c 1 = 0.88889

x 2 = - 0.77460

c 2 = 0.55556

Aplicando a fórmula com mudança do intervalo de integração:

x = 1 2 t + 1 + 0 = t + 1 2

d x = 1 2 d t

∫ 0 1 sin ⁡ x x d x = 1 2 ∫ - 1 1 sin ⁡ t + 1 2 t + 1 2 ≈ 1 2 0.55556 sin ⁡ 0.77460 + 1 2 0.77460 + 1 2 + 0.88889 sin ⁡ 0 + 1 2 0 + 1 2 + 0.55556 sin ⁡ - 0.77460 + 1 2 - 0.77460 + 1 2 = 0.94609

Resposta

a 4.66941

b 0.94609

Exercício Resolvido #4

Lista 6 – Professora Angela – UFRJ – Exercício 6

Calcular usando Quadratura Gaussiana com dois pontos o valor da integral:

∫ - 2 2 e - x 2 2 d x

Passo 1

Basta aplicarmos a fórmula lembrando de fazer a mudança de intervalo de integração:

x = 1 2 4 t + 2 - 2 = 2 t

d x = 4 2 d t = 2 d t

∫ - 2 2 e - x 2 2 d x = 2 ∫ - 1 1 exp ⁡ - 2 t 2 d t ≈ 2 exp ⁡ - 2 - 3 3 2 + exp ⁡ - 2 3 3 2 = 2.05367

Resposta

2.05367

Exercício Resolvido #5

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 233, exemplo 2 adaptado

Considere a integral ∫ 1 3 x 6 - x 2 sin ⁡ 2 x d x = 317.3442466 .

a Encontre uma aproximação para essa integral por Quadratura Gaussiana com n = 2 . Calcule o erro percentual cometido.

b Repita o item a com n = 3 .

Passo 1

Mudando o intervalo de integração:

x = 1 2 2 t + 3 + 1 = t + 2

d x = d t

∫ 1 3 x 6 - x 2 sin ⁡ 2 x d x = ∫ - 1 1 t + 2 6 - t + 2 2 sin ⁡ 2 t + 4 d t

Passo 2

a Aproximando para n = 2 :

∫ 1 3 x 6 - x 2 sin ⁡ 2 x d x ≈ - 3 3 + 2 6 - - 3 3 + 2 2 sin ⁡ 2 - 3 3 + 4 + 3 3 + 2 6 - 3 3 + 2 2 sin ⁡ 2 3 3 + 4 = 306.8199345

Calculando o erro:

E R = 306.8199345 - 317.3442466 317.3442466 × 100 = 3.32 %

Passo 3

b Aproximando para n = 3 . Lembre-se que temos, para esse caso,

x 0 = 0.77460

c 0 = 0.55556

x 1 = 0.0000

c 1 = 0.88889

x 2 = - 0.77460

c 2 = 0.55556

Então ficamos com:

∫ 1 3 x 6 - x 2 sin ⁡ 2 x d x ≈ 0.55556 0.77460 + 2 6 - 0.77460 + 2 2 sin ⁡ 2 0.77460 + 4 + 0.88889 0 + 2 6 - 0 + 2 2 sin ⁡ 2 0 + 4 + 0.55556 - 0.77460 + 2 6 - - 0.77460 + 2 2 sin ⁡ 2 - 0.77460 + 4 = 317.2680670

Calculando o erro:

E R = 317.2680670 - 317.3442466 317.3442466 × 100 = 0.024 %

Resposta

a 306.8199345

E R = 3.32 %

b 317.2680670

E R = 0.024 %

Exercícios de Livros Relacionados

Deduza a fórmula de integração da forma ∫ - 1 1 f ( x ) d x ≈ w 0 f ( - 0.5 ) + w 1 f ( 0 ) + w 2 f ( 0.5 ) que integre exatamente polinômios de grau ≤ 2.
Escolha uma regra de quadratura sobre pontos igualmente espaçados de h e avalie: ∫ − 1 0 𝑥 𝑒 𝑥 𝑑 𝑥 ,Com duas casas decimais corretas.
Calcular:Por quadratura de Gauss e diretamente e comparar os resultados.
Calcular:Por quadratura de Gauss e diretamente e comparar os resultados.