Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.6 - Ex. 33

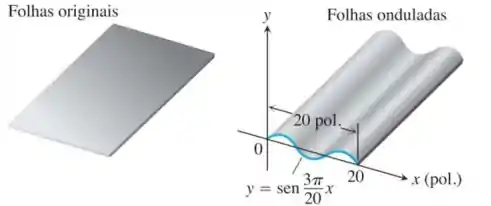
Sua empresa de fabricação de metal está tentando fechar contrato para produzir folhas onduladas de metal para telhado, como mostramos a seguir. As seções transversais dessas folhas devem se ajustar à curva

y = s e n   3 π 20   x ,       x ∈ 0,20

Se as telhas devem ser moldadas a partir de folhas planas, por um processo que não deforme o material, qual deverá ser a largura da folha original? Para descobrir, use integração numérica para aproximar o comprimento da senoide com uma precisão de duas casas decimais.

Passo 1

Aviso aos Navegantes : Essa é uma questão de integração numérica. Isso significa que precisaremos de uma calculadora em algum momento de nosso cálculo. Então nós queremos saber na real o comprimento da função s e n   3 π 20   x .

Vamos lembrar que o comprimento (   C   ) de uma função pode ser encontrada por :

C =   ∫ a b 1 + f ' x 2     d x

Então precisamos encontrar a derivada de nossa função primeiro.

Passo 2

f x =   s e n   3 π 20   x  

f ' x = cos ⁡ 3 π 20   x   * 3 π 20  

f ' x 2 =   cos 2 ⁡ 3 π 20   x   *   3 π 20 2    

Então nosso comprimento fica

C =   ∫ a b 1 + f ' x 2     d x

C =   ∫ 0 20 1 + cos 2 ⁡ 3 π 20   x   *   3 π 20 2     d x

E é essa a parte numérica. Vamos apelar para nossa calculadora.

C = 21,07   p o l → 0,54   m

Por aqui terminamos, te encontro na próxima resolução. : )

Resposta

C = 21,07   p o l → 0,54   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove que a soma T na regra do trapézio para ∫ a b f x d x é uma soma de Riemann para f contínua em [ a ,b ] . Dica: use o teorema do valor intermediário para mostrar a existência de c k no subinterva
Use a regra ⅓ de Simpson para integrar a função abaixo entre 0 e 2 com o menor esforço computacional possível(menor número de divisões e maior precisão). Justifique. Trabalhe com três casas decimais.
Determinar b, a distância entre x i e x i + 1 para que se possa avaliar ∫ 0 π / 2 c o s ( x ) d x com erro inferior a 1 0 - 3 pela regra de Simpson.
Usando a regra de Simpson, calcule o valor de ∫ 1 2 d x x com precisão de 4 casas decimais. Compare o resultado com o valor de l n ( 2 ) .
Calcule o valor aproximado de ∫ 0 0.6 d x 1 + x com três casas decimais de precisão usandoSimpsonTrapézios.