Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 6.Exercícios - Ex. 10
10. Aproxime a tabela abaixo por uma função do tipo usando mínimos quadrados. Discuta seus resultados.
Passo 1
a) E ai meu bom! Bora pra decima questão desse capítulo 6!
Se liga só! Queremos aproximar uma função dado que...
Passo 2
Sendo assim, nossa aproximação será...
Linearizando...
A tabela linearizada então, fica assim:
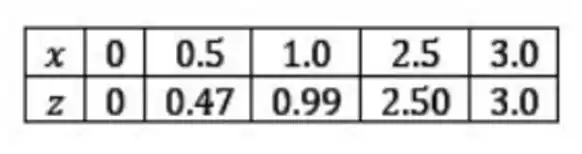
Passo 3
E temos então, os vetores...
Agora, montamos a matriz :
E o vetor :
Resolvendo o sistema:
E voltando às variáveis...
Desse modo, temos que...
Passo 4
Para discutir nosso resultado, vamos olhar para o gráfico com os pontos e a função encontrada e ver se a função serve para os pontos dados. Nosso gráfico é:
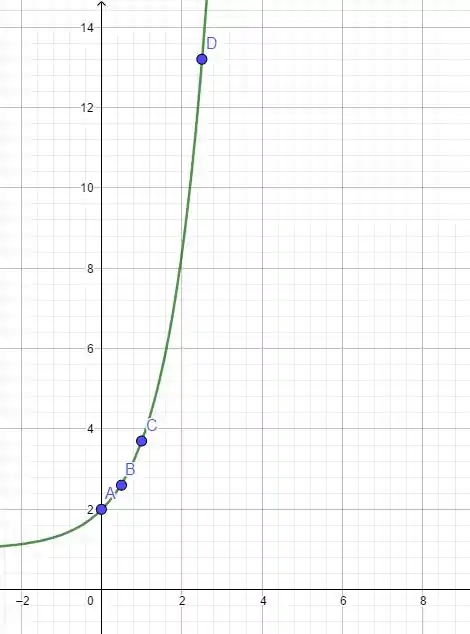
Como podemos ver, a função passa por todos os pontos da forma que queríamos!! Logo, ela realmente satisfaz esse problema. 😊
Resposta
Exercícios de Livros Relacionados
11. Considere a tabela...Por qual das funções x t = t a t + b ou y t = a b t você aproximaria a função u ( t ) ? Justifique sua resposta.
Considere a função: y t = - 1 , - π ≤ t ≤ 0 1 , 0 ≤ t ≤ π Verificar que a aproximação trigonométrica de grau 2: y t = a 0 + a 1 cos t + b 1 sin t + a 2 cos 2 t + b 2 sin 2 t Para y ( t ) é dad
Mostre que o conjunto das funções: { 1 , cos t , sin t , cos 2 t , sin 2 t ,… , sin m t } e um sistema ortogonal em [ - π , π ]
Determinar aproximação trigonométrica de ordem 2 , em [ - π , π ] , para y ( t )= | sin t | .