Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 6.Exercícios - Ex. 11

11. Considere a tabela...

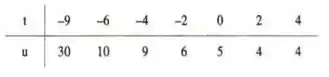
Por qual das funções x t = t a t + b ou y t = a b t você aproximaria a função u ( t ) ? Justifique sua resposta.

Passo 1

Lembra do teste que o produtor comentou aqui numa questão desse mesmo capítulo? O teste do alinhamento!

Pois bem! Chegou a hora mais uma vez de utilizá-lo!

Vamos linearizar a primeira função...

x t = t a t + b

z 1 t = 1 x ( t ) = a t + b t = a + b t

s = 1 t ⇨ z 1 t = a + b s

Isso nos dá a tabela abaixo...

Teve um probleminha ai! Em t = 0 , acabou havendo uma indeterminação, resultante da divisão por zero.

Jogando então, os pontos em um tabela de dispersão, temos que...

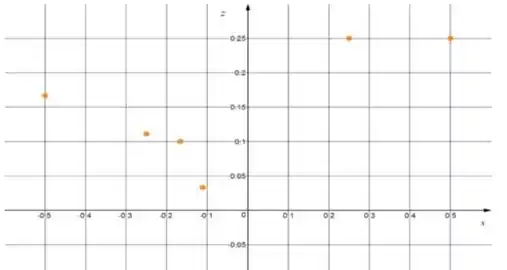
Nada haver com uma reta, né não!?

Passo 2

A outra aproximação é dada por...

y t = a b t

Linearizando...

z 2 t = ln ⁡ ( y t ) = ln ⁡ a + ln ⁡ b t = ln ⁡ a ⏟ c 1 + l ln ⁡ b ⏟ c 2 = c 1 + c 2 t

Chegamos até a tabela abaixo...

Que nos dá o seguinte diagrama de dispersão...

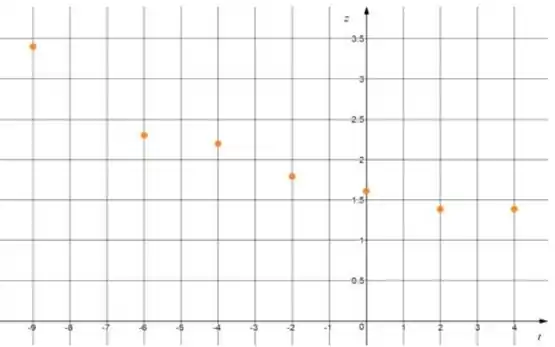
Bom! Nada é perfeito nesse mundo, né!? Mas eu posso dizer com certeza, que esses pontos ai estão mais próximos de formar uma reta que os da imagem anterior. Sendo assim, ficamos com y t = a b t . É a melhor função para aproximar u ( t ) !

Resposta

y t = a b t   a p r o x i m a   m e l h o r   u ( t )   p e l o   t e s t e   d o   a l i n h a m e n t o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dada a tabela abaixo, faça o gráfico de dispersão dos dados e ajuste uma curva da melhor maneira possível:
9. a) Considere:Através do teste de alinhamento, escolha uma das famílias de funções abaixo que melhor ajuste estes dados: a e b x , 1 / ( a + b x ) , x / ( a + b x ) b) Ajuste os dados do item acima
10. Aproxime a tabela abaixo por uma função do tipo g x = 1 + a e b x usando mínimos quadrados. Discuta seus resultados.
Obter aproximação trigonométrica, de ordem 1 , para a função:
Deseja-se aproximar uma função f0 tabelada por uma função do tipo: x 2 ln ⁡ ( a x 4 + b x 2 + c ) usando o método dos mínimos quadrados.a) Podemos aproximar f diretamente pela função acima? Caso não s