Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 7.Exercícios - Ex. 14
14. Calcule pela regra dos trapézios e de Simpson cada uma das integrais abaixo, com erro menor do que dado:
a)
b)
Passo 1
a) Vamos usar a regra de de Simpson!
Bom! Vamos ver quantos intervalos a gente precisa usar, considerando uma precisão de casas decimais...
A derivada terceira de...
Com indo de até ...
Sendo assim, vamos pegar um valor de por exemplo!
Passo 2
E agora, vamos montar a tabela abaixo...
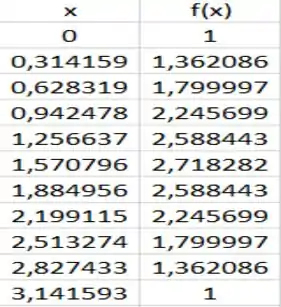
Calculando a integral...
O valor exato sua vez, é dado por...
O que nos dá um erro de...
Passo 3
b) Para esse segundo caso, temos que...
Com passos, temos que...
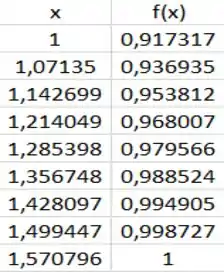
Desse modo, temos que...
O valor exato, nós sabemos que é dado por...
Garantindo um erro de...
Resposta
a)
b)
Exercícios de Livros Relacionados
Ache os limitantes para o erro de truncamento na aproximação do exercício indicado. ∫ - 1 0 d x 1 - x ; n=4.
Ache o limitante para o erro de truncamento na aproximação do exercício indicado: ∫ 0 2 x 3 d x ; n = 4
A integral a seguir não pode ser calculada exatamente em termos das funções elementares. Use a regra de Simpsom com o valor indicado n para encontrar um valor aproximado da integral definida dada. Exp
A integral a seguir não pode ser calculada exatamente em termos das funções elementares. Use a regra de Simpsom com o valor indicado n para encontrar um valor aproximado da integral definida dada. Exp
A integral a seguir não pode ser calculada exatamente em termos das funções elementares. Use a regra de Simpsom com o valor indicado n para encontrar um valor aproximado da integral definida dada. Exp