Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 15

15. Calcule y ( 1 ) para y ' = y - x ; y 0 = 2 , utilizando Euler e Runge-Kutta de 4 ª ordem com h = 0.2 . Comparar seus resultados com os valores exatos de y ( x ) nos pontos x i , sabendo que y x = e x + x + 1 .

Passo 1

E aí meus caros e caras!

Se liga só! O PVI do exercício 15 é dado por...

y ' = y - x y 0 = 2    

E o que a questão pede é pra gente resolver ele usando outros métodos e vários valores de h . O que nós temos que fazer aqui é achar o y ( 1.0 ) ... Por isso, vamos recorrer aos métodos de Euler, Runge-Kutta de 4 ª ordem.

Passo 2

Chamando então y ' de f ( x n , y n ) , temos para o método de Euler, a seguinte fórmula de recorrência...

y n + 1 = y n + h f ( x n , y n )

y n + 1 = y n + h ( y n - x n )

y n + 1 = y n + h ( y n - n h )

E fazendo um código em linguagem C para isso, chegamos ao exposto na seguinte imagem abaixo, para h = 0.2 ;

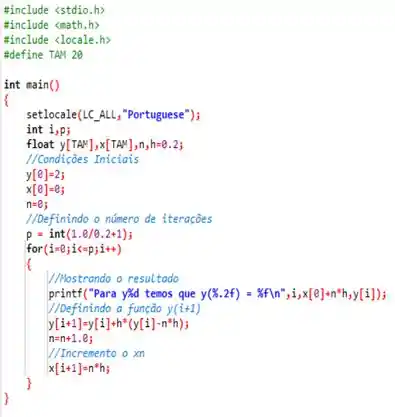
Compilando ele, obtemos que...

y 1.0 ≅ 4.488320

Passo 3

Por último, vamos recorrer ao meu amigo Runge-Kutta de 4 ª ordem...

A fórmula de recorrência do método de Runge-Kutta de 4 ª ordem é dada por...

y n + 1 = 1 6 ( k 1 n + 2 k 2 n + 2 k 3 n + k 4 n )

Sendo assim, chamando y ' d e f x n , y n , temos para k 1 n

  k 1 ( n ) = h f ( x n , y n )

k 1 n = h ( y n - n h )

k 2 n = h f x n + h 2 , y n + k 1 ( n ) 2

k 2 n = h y n + k 1 ( n ) 2 - n h - h 2

k 3 n = h f x n + h 2 , y n + k 2 n 2

k 3 n = h y n + k 2 ( n ) 2 - n h - h 2

k 4 n = h f x n + h 2 , y n + k 3 n 2

k 4 n = h y n + k 3 ( n ) 2 - n h - h 2

E mais uma vez dando uma modificada no nosso código, obtemos para h = 0.2 que...

y 1.0 ≅ 4.718251

Passo 4

Agora, vamos ver qual o valor real de y ( 1.0 ) através da solução conhecida da E D O ...

y x = e x + x + 1

Substituindo x = 1.0 ;

y x = e x + x + 1

y 1.0 = e 1.0 + 1.0 + 1

y 1.0 = 4.718281

Resposta

E u l e r → y 1.0 ≅ 4.488320

R u n g e - K u t t a   d e   4 ª   o r d e m → y 1.0 ≅ 4.718251

S o l u ç ã o   e x a t a → y 1.0 = 4.718281

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule y ( 1 ) para y ' = y - x ,y ( 0 ) = 2 , utilizando Euler e Runge-Kutta de 4º ordem com h=0.2. Comparar seus resultados com os valores exatos de y(x) nos pontos x i , sabendo que y ( x ) = e x
10. Substitua y ' ( x ) jo PVI abaixo por y x + h - y x / h e obtenha uma equação diferencial de diferenças para aproximar a solução da equação diferencial.Faça h = 0.2 e h = 0.1 e encontre, em cada c
11. Use a aproximação do exercício 10 para o problema do exercício 3
14. Resolva o PVI do exercício 10 por outros métodos e vários valores de h