Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 11
11. Use a aproximação do exercício 10 para o problema do exercício 3
Passo 1
Se liga só! Vamos usar o método de Runge-Kutta de ordem pra resolver essa equação...
Sabemos que a equação que o problema quer que a gente analise é dada por...
Pois bem! Chamando de ... Temos que...
A fórmula de recorrência do método de Runge-Kutta de ordem é dada por...
Sendo assim, chamando , temos que a nossa fórmula vai ficar...
Passo 2
Desse modo, utilizando uma ferramenta computacional...
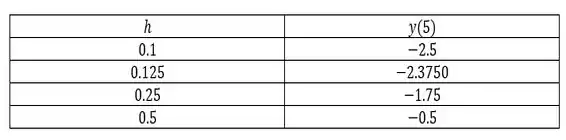
Para cada um dos passos que nos foi fornecido no enunciado, chegamos até a seguinte tabela abaixo...
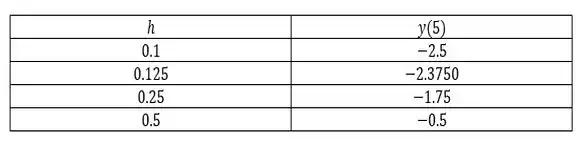
Resposta
Exercícios de Livros Relacionados
Calcule y ( 1 ) para y ' = y - x ,y ( 0 ) = 2 , utilizando Euler e Runge-Kutta de 4º ordem com h=0.2. Comparar seus resultados com os valores exatos de y(x) nos pontos x i , sabendo que y ( x ) = e x
2. O problema de valor inicial y ' = - 20 y y 0 = 1 ,t e mp o rú n i c as o l u ç ã oe x a t ay x = e - 20 x ú çã a) Verifique a afirmação acimab) Verifique que qualquer método de Runge-Kutta de 2ª or
10. Substitua y ' ( x ) jo PVI abaixo por y x + h - y x / h e obtenha uma equação diferencial de diferenças para aproximar a solução da equação diferencial.Faça h = 0.2 e h = 0.1 e encontre, em cada c
14. Resolva o PVI do exercício 10 por outros métodos e vários valores de h
15. Calcule y ( 1 ) para y ' = y - x ; y 0 = 2 , utilizando Euler e Runge-Kutta de 4 ª ª ordem com h = 0.2 . Comparar seus resultados com os valores exatos de y ( x ) nos pontos x i , sabendo que y x