Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 15

Calcule y ( 1 ) para y ' = y - x ,   y ( 0 ) = 2 , utilizando Euler e Runge-Kutta de 4º ordem com h=0.2. Comparar seus resultados com os valores exatos de y(x) nos pontos x i , sabendo que y ( x ) = e x + x + 1

Passo 1

Temos:

y ' = y - x

y 0 = 2

x 0 = 0

E com passo h=0.2 teremos o seguinte:

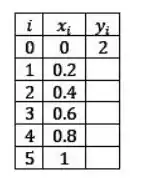
Agora é só jogar na fórmula:

Passo 2

Iteração 1 (x=0.2):

k 1 ( 0 ) = h f ( x 0 , y 0 ) = h ( y 0 - x 0 ) = 0.4

k 2 ( 0 ) = h f ( x 0 + h 2 , y 0 + k 1 ( 0 ) 2 ) = h ( ( y 0 + k 1 ( 0 ) 2 ) - ( x 0 + h 2 ) ) = 0.42

k 3 ( 0 ) = h f ( x 0 + h 2 , y 0 + k 2 ( 0 ) 2 ) = h ( ( y 0 + k 2 ( 0 ) 2 ) - ( x 0 + h 2 ) ) = 0.422

k 4 ( 0 ) = h f ( x 0 + h , y 0 + k 3 ( 0 ) ) = h ( ( y 0 + k 3 ( 0 ) ) - ( x 0 + h ) ) = 0.4444

y 1 = y 0 + 1 6 ( k 1 ( 0 ) + 2 k 2 ( 0 ) + 2 k 3 ( 0 ) + k 4 ( 0 ) ) = 2.4214

Passo 3

Iteração 2 (x=0.4):

k 1 ( 1 ) = h f ( x 1 , y 1 ) = h ( y 1 - x 1 ) = 0.44428

k 2 ( 1 ) = h f ( x 1 + h 2 , y 1 + k 1 ( 1 ) 2 ) = h ( ( y 1 + k 1 ( 1 ) 2 ) - ( x 1 + h 2 ) ) = 0.46871

k 3 ( 1 ) = h f ( x 1 + h 2 , y 1 + k 2 ( 1 ) 2 ) = h ( ( y 1 + k 2 ( 1 ) 2 ) - ( x 1 + h 2 ) ) = 0.47115

k 4 ( 1 ) = h f ( x 1 + h , y 1 + k 3 ( 1 ) ) = h ( ( y 1 + k 3 ( 1 ) ) - ( x 1 + h ) ) = 0.49851

y 2 = y 1 + 1 6 ( k 1 ( 1 ) + 2 k 2 ( 1 ) + 2 k 3 ( 1 ) + k 4 ( 1 ) ) = 2.89182

Passo 4

Iteração 3 (x=0.6):

Já deu pra entender né!

k 1 ( 2 ) = 0.49836

k 2 ( 2 ) = 0.5282

k 3 ( 2 ) = 0.53118

k 4 ( 2 ) = 0.56460

y 3 = 3.42211

Passo 5

Iteração 4 (x=0.8):

k 1 ( 3 ) = 0.56442

k 2 ( 3 ) = 0.60086

k 3 ( 3 ) = 0.60451

k 4 ( 3 ) = 0.64532

y 3 = 4.02552

Passo 6

Iteração 5 (x=1):

k 1 ( 4 ) = 0.64510

k 2 ( 4 ) = 0.68961

k 3 ( 4 ) = 0.69407

k 4 ( 4 ) = 0.74392

y 3 = 4.71825

Logo, a aproximação é:

y ( 1 ) ≈ 4.71825

Passo 7

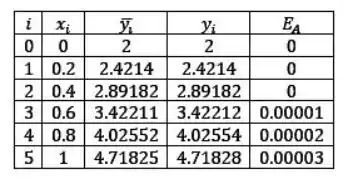
Pra fechar o exercício podemos acrescentar mais duas colunas na nossa tabela. Uma com os valores exatos encontrados por meio de y = e x + x + 1 e a outra com o erro absoluto.

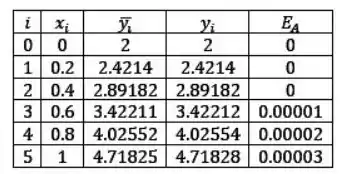
Vale ressaltar que o erro 0 obtido para y(0.2) e y(0.4) indica que, trabalhando com 5 casas decimais, o erro é de zero. No entanto, ele ainda existe, apenas é menor que 1 0 - 5 !

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2. O problema de valor inicial y ' = - 20 y y 0 = 1 ,t e mp o rú n i c as o l u ç ã oe x a t ay x = e - 20 x ú çã a) Verifique a afirmação acimab) Verifique que qualquer método de Runge-Kutta de 2ª or
10. Substitua y ' ( x ) jo PVI abaixo por y x + h - y x / h e obtenha uma equação diferencial de diferenças para aproximar a solução da equação diferencial.Faça h = 0.2 e h = 0.1 e encontre, em cada c
11. Use a aproximação do exercício 10 para o problema do exercício 3
14. Resolva o PVI do exercício 10 por outros métodos e vários valores de h
15. Calcule y ( 1 ) para y ' = y - x ; y 0 = 2 , utilizando Euler e Runge-Kutta de 4 ª ª ordem com h = 0.2 . Comparar seus resultados com os valores exatos de y ( x ) nos pontos x i , sabendo que y x