Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 3.Exercícios - Ex. 6.a
Analise os sistemas lineares abaixo com relação ao número de soluções, usando o método da Eliminação de Gauss (trabalhe com três casas decimais):
Passo 1
Eai pessoal, vamos escrever um passo-a-passo, pra ficar mais fácil!
Passo 2
A gente tem essa matriz daqui:
Primeiro passo vai ser:
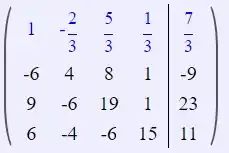
Passo 3
Agora, faremos:
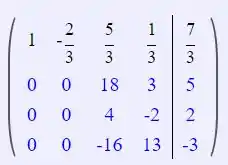
Passo 4
Agora, faremos:
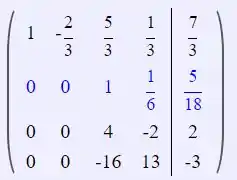
Passo 5
Agora:
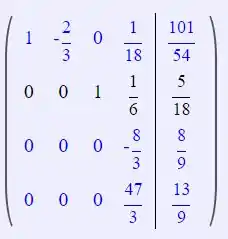
Passo 6
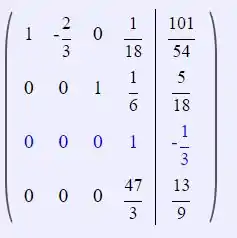
Passo 7
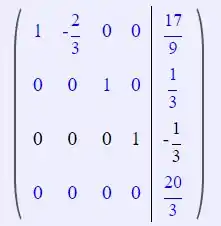
Opa mas essa última linha ta falando que , o que é impossível!
Resposta
O sistema não tem solução, já que
Exercícios de Livros Relacionados
Para cada um dos sistemas lineares a seguir, analise a existência ou não de solução, bem como unicidade de solução, no caso de haver existência.
O cálculo do determinante de matrizes quadradas pode ser feito usando o método da Eliminação de Gauss.Deduza o método.Aplique-o no cálculo do determinante das matrizes dos sistemas dos Exercícios 5 e
Analise os sistemas lineares abaixo com relação ao número de soluções, usando o método da Eliminação de Gauss (trabalhe com três casas decimais):
O cálculo do determinante de matrizes quadradas pode ser feito usando o método da Eliminação de Gauss.Deduza o método.Aplique-o no cálculo do determinante das matrizes dos sistemas dos Exercícios 5 e
O cálculo do determinante de matrizes quadradas pode ser feito usando o método da Eliminação de Gauss.Deduza o método.Aplique-o no cálculo do determinante das matrizes dos sistemas dos Exercícios 5 e