Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 3.Exercícios - Ex. 7.b
O cálculo do determinante de matrizes quadradas pode ser feito usando o método da Eliminação de Gauss.
- Deduza o método.
- Aplique-o no cálculo do determinante das matrizes dos sistemas dos Exercícios 5 e 6.
- Inclua o cálculo do determinante da matriz A do sistema AX=b no algoritmo do método da Eliminação de Gauss.
Passo 1
Eai pessoal, vamo nessa, resolver isso daqui rapidinho!
Passo 2
A matriz da equação 5 é essa daqui ó:
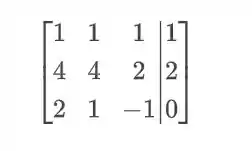
Passo 3
Vamos começar agora o método, a primeira fase é a Eliminação!
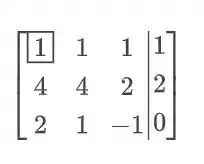
Agora vamos substituir
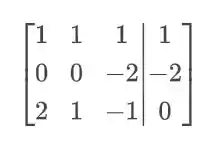
Agora vamos trocar a segunda pela terceira linha: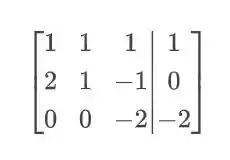
Agora vamos jogar , na segunda linha:
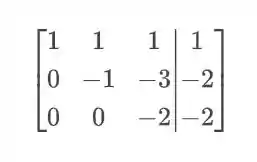
Passo 4
Se a gente chamar de , a matrix:
Podemos fazer então,
Temos então que:
Passo 5
As matrizes da equação 6, são chamadas de.
Vimos que elas tem uma linha de zeros, logo o determinante vai ser zero!
Resposta
Exercícios de Livros Relacionados
Para cada um dos sistemas lineares a seguir, analise a existência ou não de solução, bem como unicidade de solução, no caso de haver existência.
Para cada um dos sistemas lineares a seguir, analise a existência ou não de solução, bem como unicidade de solução, no caso de haver existência.
Para cada um dos sistemas lineares a seguir, analise a existência ou não de solução, bem como unicidade de solução, no caso de haver existência.
Para cada um dos sistemas lineares a seguir, analise a existência ou não de solução, bem como unicidade de solução, no caso de haver existência.
Para cada um dos sistemas lineares a seguir, analise a existência ou não de solução, bem como unicidade de solução, no caso de haver existência.