O cálculo do determinante de matrizes quadradas pode ser feito usando o método da Eliminação de Gauss.

1. Deduza o método.
2. Aplique-o no cálculo do determinante das matrizes dos sistemas dos Exercícios 5 e 6.
3. Inclua o cálculo do determinante da matriz A do sistema X=b no algoritmo do método da Eliminação de Gauss.

Então, digamos que a gente tenha uma matriz nesse formato daqui

Depois de todos os passos da Eliminação de Gauss, a gente vai ter a matriz assim:

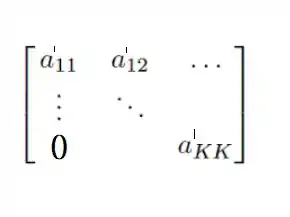
Temos um número de troca de linhas feitas durante o método é:

Sabemos que as outras operações substituem a linha pelo valor dela mesma subtraido de uma constante vezes alguma outra linha, ou seja, não modificam o determinante!

Agora todos os termos abaixo da diagonal principal vão ser zero, o resultado do determinante então será a multiplicação de todos os valores da diagonal principal, desse jeito aqui:

Esse fator de -1 aparece aí pq a cada vez que a gente troca de linha, o sinal é invertido!