Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 2.Exercícios - Ex. 5
Ao se aplicar o método do ponto fixo (MPF) à resolução de uma equação, obtivemos os seguintes resultados nas iterações indicadas:
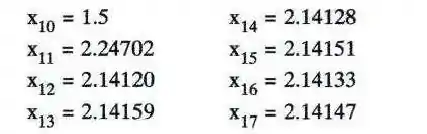
Escreva o que puder a respeito da raiz procurada.
Passo 1
Sabemos que a sequência oscila em torno de uma raiz, então o método MPF converge!
Passo 2
Como a sequência está convergindo, então para a gente obter a melhor precisão nessa raiz, podemos fazer uma média do e e usar como .
Fora isso, temos que calcular o valor do erro máximo dessa nossa estimação, que vai ser metade do intervalo .
Passo 3
Calculando tudo, a gente tem:
Resposta
Exercícios de Livros Relacionados
Considere a função f(x) = x3 - x - 1 (do Exemplo 19). Resolva-a pelo MPF com função de iteração φ ( x ) = 1 x + 1 x 2 e x 0 = 1 . Justifique seus resultados.
A equação x 2 - b = 0 tem como raiz ξ = b . Considere o MPF com φ ( x ) = b x : Comprove que φ ' ( ξ ) =- 1 ; o que acontece com a sequência { x k } tal que x k + 1 = φ ( x k ) ? sua conclusão do item
9. Se a função de iteração do MPF for tal que as condições do Teorema 2 estão satisfeitas:a) mostre que ξ - x kM 1 - M x k - x k - 1 ;b) para que valores de M teremos então que ξ - x kε se x k - x k -