Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios - Ex. 1

Aplicar a regra do trapézio para calcular:

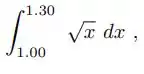
Utilizando os dados da tabela a seguir:

Passo 1

Eaí, tudo beleza? Vamos utilizar a regra do trapézio simples para calcular a integral. A fórmula é a seguinte:

h 2 𝑦 0 + 𝑦 1

Porém, o exercício nos deu uma tabela que não contém apenas um subintervalo 𝑦 0   , 𝑦 1 , portanto teremos que mexer na fórmula para deixá-la apropriada para a tabela, que tem seis subintervalos. Mudando a fórmula teremos:

h 2 𝑦 0 + 𝑦 1 + h 2 𝑦 1 + 𝑦 2 + h 2 𝑦 2 + 𝑦 3 + h 2 𝑦 3 + 𝑦 4 + h 2 𝑦 4 + 𝑦 5 + h 2 𝑦 5 + 𝑦 6

Simplificando:

h 2 𝑦 0 + 2 𝑦 1 + 2 𝑦 2 + 2 𝑦 3 + 2 𝑦 4 + 2 𝑦 5 + 𝑦 6

Passo 2

Agora só precisamos substituir os valores e calcular o passo (h):

Calculando o passo:

h = 1.3 − 1 6 = 0.05

Substituindo os valores por auxílio da tabela:

0.05 2 1.000 + 2 1.0247 + 2 1.0488 + 2 1.0723 + 2 1.0954 + 2 1.1180 + 1.1401 = 0.3214625

E com isso, achamos o valor da integral definida!

Resposta

Valor da integral = 0.3214625   .

Exercícios de Livros Relacionados

Calcular:Pela regra do trapézio, com h = 0.4, 0.2 e 0.1, sabendo que
Obtenha a fórmula de integração de Newton-cotes do tipo fechado, para integrar f(x), com n = 4, ou seja, sobre 5 pontos. Usando a fórmula obtida aproxime:Sabendo que
Considere a integral:Justifique o porquê da regra do trapézio, com h=1 ser exata para calcular tal integral.
Uma maneira de se obter numericamente valores da função 𝑓 𝑥 = l n l n𝑥 é calcular numericamente valores da integral: l n l n𝑥= ∫ 1 𝑥 𝑑 𝑡 𝑡 ,Calcular:I) l n l n   1.7
Considere a integral: 𝐼   =   ∫ 0 0.8 𝑥 2 − c o s c o s𝑥𝑑 𝑥     a) Quantos intervalos seriam necessários para aproximar 𝐼    usando a regra do trapézio, com erro inferior a 10 − 2 .