Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios - Ex. 2
Calcular:
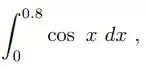
Pela regra do trapézio, com h = 0.4, 0.2 e 0.1, sabendo que
Passo 1
Eaí, tudo beleza? Vamos utilizar a regra do trapézio para calcular a integral. A fórmula é a seguinte:
Porém, o exercício nos deu uma tabela que não contém apenas um subintervalo , portanto teremos que mexer na fórmula para deixá-la apropriada de acordo com o passo (h) que o exercício nos forneceu. Considere que cada valor de x tem um índice, sendo x = 0 índice 0 e x = 0.8 índice 8, assim fica mais fácil você saber que , por exemplo, é o valor de quando x = 0, que foi dado na tabela com valor 1.
Para h = 0.4:
Para h = 0.2:
Para h = 0.1:
Passo 2
Resolvendo cada expressão:
Para h = 0.4:
Para h = 0.2:
Para h = 0.1:
Consegue perceber que, quanto menor o passo, mais subintervalos teremos e maior será a precisão do resultado?
Resposta
Para h = 0.4, 0.2 e 0.1, obtemos 0.7076, 0.7148 e 0.7165 respectivamente.