Considere a integral:

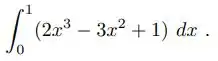
Justifique o porquê da regra do trapézio, com h=1 ser exata para calcular tal integral.

Salve! Tudo tranquilo? Para resolver o exercício, considere a seguinte imagem:

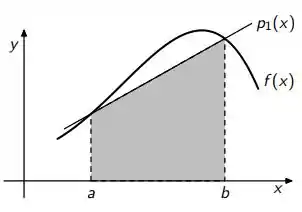
Perceba que a regra do trapézio pode ser entendida como exata para o polinômio interpolador entre os extremos do intervalo de integração (p(x)), por isso podemos dizer que, geralmente, em casos assim, a regra do trapézio terá erro zero, visto que o polinômio interpolador tem grau 1 e trabalhamos com derivada segunda na fórmula do erro, o que implica que existirá uma multiplicação por zero ocasionando no erro ser igual a zero.