Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 7.Exercícios - Ex. 1

Calcule as integrais a seguir pela regra dos Trapézios usando quatro e seis divisões de [a,b].

  1. ∫ 1 2 e x d x
  2. ∫ 1 4 x d x
  3. ∫ 2 14 d x x

Passo 1

letra a:

∫ 1 2 e x d x

Então temos h = 1 4 = 0.25

Vamos montar a tabelinha:

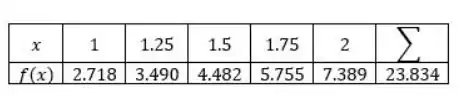
Agora é só aplicar na fórmula (Trapézios):

∫ 1 2 e x d x ≈ 0.25 2 [ 2 ( 23.834 ) - 2.718 - 7.389 ] = 4.695

E agora (Simpson):

∫ 1 2 e x d x ≈ 0.25 3 f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + f x 4

= 0.25 3 2.718 + 4 3.490 + 2 4.482 + 4 5.755 + 7.389

= 4.671

Passo 2

Para 6 divisões;

Agora, h = 1 6 = 0.167

Vamos montar a tabelinha:

E aplicamos a fórmula (Trapézio):

∫ 1 2 e x d x   ≈ 0.167 2 [ 2 ( 33.143 ) - 2.718 - 7.389 ] = 4.691

E agora (Simpson):

∫ 1 2 e x d x ≈ 0.167 3 f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + 2 f x 4 + 4 f x 5 + f x 6

= 0.167 3 2.718 + 4 3.211 + 2 3.794 + 4 4.482 + 2 5.294 + 4 6.255 + 7.389

= 4.680

Passo 3

Agora na letra b:

∫ 1 4 x d x

Temos que h = 3 4 = 0.75 , montando a tabela…

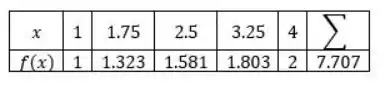
Agora na fórmula:

∫ 1 4 x d x ≈ 0.75 2 [ 2 ( 7.707 ) - 1 - 2 ] = 4.655

E agora (Simpson):

∫ 1 4 x d x ≈ 0.75 3 f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + f x 4

= 0.75 3 1 + 4 1.323 + 2 1.581 + 4 1.803 + 2

= 4.667

Passo 4

Agora h = 3 6 = 0.5 , na tabela:

Aplicando agora a fórmula:

∫ 1 4 x d x ≈ 0.5 2 2 10.823 - 1 - 2 = 4.662

E agora (Simpson):

∫ 1 4 x d x ≈ 0.5 3 f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + 2 f x 4 + 4 f x 5 + f x 6

= 0.5 3 1 + 4 1.225 + 2 1.414 + 4 1.581 + 2 1.732 + 4 1.871 + 2

= 4.667

Passo 5

Agora na letra c:

∫ 2 14 d x x

h = 12 4 = 3 ,   n a   t a b e l a :

(Trapézio):

∫ 2 14 d x x   ≈   3 2 [ 2 ( 2.077 ) - 0.707 - 0.267 ] = 4.770

E agora (Simpson):

∫ 2 14 1 x d x ≈ 3 3 f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + f x 4

= 3 3 0.707 + 4 0.447 + 2 0.354 + 4 0.302 + 0.267

= 4.678

Passo 6

Agora para 6 divisões:

Temos h = 12 6 = 2 . Na tabela:

(Trapézio):

∫ 2 14 d x x ≈ 2 2 [ 2 ( 2.841 ) - 0.707 - 0.267 ] = 4.708

E agora (Simpson):

∫ 2 14 x d x ≈ 2 3 f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + 2 f x 4 + 4 f x 5 + f x 6

= 2 3 0.707 + 4 0.5 + 2 0.408 + 4 0.354 + 2 0.316 + 4 0.289 + 0.267

= 4.663

Resposta

  1. 4   d i v : 4.695

    2. 6   d i v : 4.691  

  2. 4   d i v : 4.655

    3. 6   d i v : 4.662  

  3. 4   d i v : 4.770

6   d i v : 4.708  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual o erro máximo cometido na aproximação de ∫ 0 4 ( 3 x 3 - 3 x + 1 ) d x pela regra dos Trapézios com quatro subintervalos?
Usando as integrais do exercício anterior com quantas divisões do intervalo, no mínimo, podemos esperar obter erros menores que 1 0 - 5 ?
Em que sentido a regra de Simpson é melhor do que a regra dos Trapézios?
11. a) Comprove gráfica e analiticamente que se:i) f ' ' ( x ) é contínua em [ a , b ] , eii) f ' ' x0 , ∀ x ∈ [ a , b ] ,então, a aproximação obtida para ∫ a b f x d x pela regra dos Trapézios é maio