11. a) Comprove gráfica e analiticamente que se:
i) é contínua em , e
ii) ,
então, a aproximação obtida para pela regra dos Trapézios é maior do que o valor exato da . Considere .
b) Sabendo que satisfaz as condições acima em , e que , comprove que a conclusão do item (a) é válida também para a regra dos Trapézios repetida, calculando com erro inferior a . Use três casas decimais.
Passo 1
a) E aí meu bom! Se liga só!
O erro da regra dos Trapézios envolve a segunda derivada , nos dando o resultado exato quando aplicada a qualquer função cuja segunda derivada seja igual a zero, ou seja, para qualquer função com grau 1 ou menos. Se a segunda derivada der igual a zero, o valor fica mais aproximado do que utilizando o cálculo da integral propriamente dita.
Como vimos, a regra dos trapézios faz uso de uma aproximação de uma função por meio de uma reta. A aproximação da integral desejada é feita a partir da área do trapézio obtido. Ao aplicar diversas vezes esta regra em um intervalo , ela adequa-se melhor ao cálculo da integral, sendo uma técnica mais refinada em relação à simples aproximação da área por um trapézio e muito útil quando temos uma função com grau maior que e desejamos, ainda assim, a aproximação por trapézios.
Passo 2
No caso abaixo, a integral de pode ser aproximada pela área de um único trapézio. Deste modo, observa-se que quanto menor a altura h do trapézio no intervalo , indicada na imagem abaixo, melhor será a aproximação.
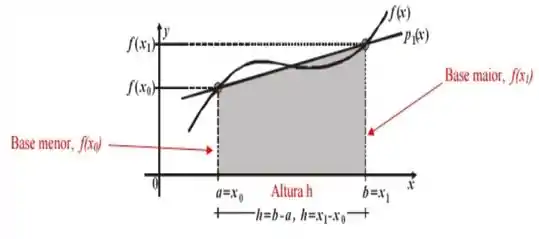
Dependendo do intervalo/altura utilizada, a aproximação pode ser grosseira. Para melhorarmos tal relação, restringimos o intervalo a um certo tamanho e aplicamos a regra do trapézio repetidas vezes, tomando muitos trapézios com altura tendendo a zero para que a aproximação seja a mais adequada para a função, como mostra a imagem:
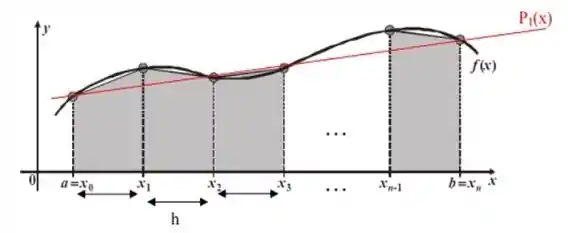
Nesse caso, a segunda derivada da função é maior que zero, o que faz com que a aproximação seja melhor com o uso dos trapézios do que com os retângulos propriamente ditos.
Passo 3
b) Agora, vamos recorrer à regra dos trapézios repetida.
Primeiro, vamos ver o número de subintervalos pra usar...
Sendo que...
A segunda derivada da função , é dada por...
Calculando e :
Podemos ver que o valor máximo é...
Sendo assim...
Peguemos então !
Logo...
Passo 4
Assim, obtemos a tabela abaixo...
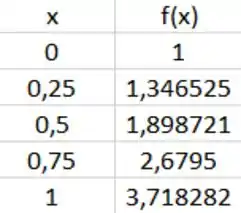
E então, calculando a integral, temos que...
Obtendo então, nossa resposta!
Resposta
a)
b)