Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 25

Formule, por diferenças finitas, sistemas de equações cuja solução aproxime a solução dos seguintes problemas de contorno:

  1. y ' ' = y s e n ( y ) + t y

    2. y ( 0 ) = 1

    y ( 1 ) = 5

  2. y ' ' = 2 y + y 3 - t

y ( 0 ) = 4

y ( 6 ) = 2

Passo 1

Letra a:

Vamos fazer para h=1.

Então, y 0 = y ( 0 )

y 1 = y ( 1 )

y n = y ( n ) ,   n ∈ N

Primeiro, sabemos que:

y ' ' ( t ) = y ( t + h ) - 2 y ( t ) + y ( t + h ) h 2

Então,

y ( t + h ) - 2 y ( t ) + y ( t - h ) h 2 = y ( t ) s e n ( y ) ( t ) + t y ( t )

Passo 2

Em seguida, teremos:

y ( t + h ) - 2 y ( t ) + y ( t - h ) = y ( t ) s e n ( y ( t ) ) + t y ( y )

y n + 1 = y n ( 2 + s e n ( y n ) + t ) - y n - 1 , ∀ n ≥ 2

Passo 3

Agora, na letra b:

Se vc olhar bem, existe um y 3 na EDO, que significa que o sistema que a gente vai obter é não linear.

Vamos fazer a tabela:

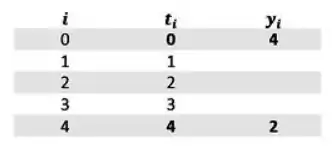
E substituir na EDO as derivadas numéricas:

Para h=1:

y ' ' = y s e n ( y ) + t y

y i + 1 - 2 y I + y I - 1 h 2 = 2 y i + y i 3 - t i

Chegaremos nas seguintes equações:

Para i=1:

y 2 - y 1 ( 2 + ( 2 + y i 2 ) ) + y 0 =   - t 1

Para i=2:

y 3 - y 2 ( 2 + ( 2 + y 2 2 ) ) + y 1 =   - t 2

Para i=3:

y 4 - y 3 ( 2 + ( 2 + y 3 2 ) ) + y 2 =   - t 3

Da tabela que nós montamos sabemos que y 4 = 2 e t 3 = 3 , então podemos substituir esse valores na equação.

- y 3 ( 4 + y 3 2 ) ) + y 2 =   - 5

Resposta

  1. y n + 1 = y n ( 2 + s e n ( y n ) + t ) - y n - 1 , ∀ n ≥ 2
  2. - y 3 ( 4 + y 3 2 ) ) + y 2 =   - 5
  3. y 2 - y 1 ( 4 + y 1 2 ) =   - 5

y 3 - y 2 ( 4 + y 2 2 ) + y 1 =   - 2

- y 3 ( 4 + y 3 2 ) ) + y 2 =   - 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja a configuração nodal 3 da tabela 4.2 . Deduza as equações de diferenças finitas, para condições de regime estacionário, nas seguintes situações.(a) O contorno está isolado. Explique como a equaçã
Seja a configuração nodal 2 da tabela 4.2 . Deduza as equações de diferenças finitas, para condições de regime estacionário, nas seguintes situações.(a) O contorno horizontal do vértice interno está p
Em uma configuração cilíndrica bidimensional, os espaçamentos radiais ( ∆ r ) e angulares ( ∆ φ ) entre os pontos nodais são uniformes. O contorno em r = r , está em uma temperatura uniforme T i . Na
Materiais funcionalmente graduados são intencionalmente fabricados para estabelecerem uma distribuição espacial de propriedades no produto final. Seja um objeto L × L bidimensional, com L = 20 mm. A d
Um canal por onde passam gases quentes de exaustão apresenta uma seção transversal quadrada de 300 mm de lado. As paredes são construídas com tijolos refratários com 150 mm de espessura e condutividad