Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 24
Resolva pelo método de diferenças finitas, o PVC
usando h = 0.25.
Passo 1
Temos o seguinte:
E teremos n intervalos de modo que:
Então, vai ficar assim:
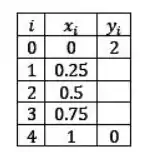
Agora vamos substituir as derivadas na nossa EDO:
E para cada i, vamos chegar no seguinte sistema:
Passo 2
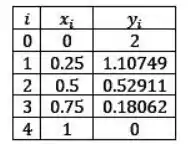
Agora, é só resolver esse sistema:
Completando o quadrinho, temos:
Resposta
Exercícios de Livros Relacionados
Determine as expressões para q ( m - 1 , n ) → ( m , n ) ,q m + 1 , n → ( m , n ) ,q m ,n + 1 → ( m , n ) e q m ,n - 1 → ( m , n ) , na condução associada a um volume de controle que abrange dois dife
Deduza as equações de diferenças finitas nodais para as seguintes considerações.(a) Nó (m,n) sobre um contorno diagonal sujeito à convecção com um fluido a uma temperatura T ∞ , com um coeficiente de
Seja uma aleta unidimensional, com área de seção transversal uniforme, isolada na sua extremidade, x = L . A temperatura na base da aleta T b e a do fluido vizinho T ∞ , bem como o coeficiente de tran
Considere a rede para um sistema bidimensional, sem geração volumétrica interna de calor, que tem as temperaturas nodais mostradas a seguir. Sendo o espaçamento da malha de 125m m e a condutividade té
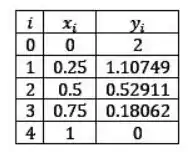
Seja o ponto nodal 0 localizado na fronteira entre materiais com condutividades térmicas k A e k B .Deduza a equação de diferenças finitas, considerando a ausência de geração interna.