Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 6.Exercícios - Ex. 9

9. a) Considere:

Através do teste de alinhamento, escolha uma das famílias de funções abaixo que melhor ajuste estes dados: a e b x , 1 / ( a + b x ) , x / ( a + b x )

b) Ajuste os dados do item acima a família de funções escolhida. Qual o resíduo minimizado!

Passo 1

a) E ai meu bom! Bora pra nona questão desse capítulo 6!

Se liga só! Vamos testar cada uma das funções que nos foram propostas!

Pois muito bem! A primeira é dada por...

y 1 = a e b x

Com base em uma variável auxiliar z 1 , linearizando, ficamos com...

z 1 = ln ⁡ y 1 = ln ⁡ a e b x = ln ⁡ a + ln ⁡ e b x = ln ⁡ a ⏟ a 1 + b ⏟ a 2 x = a 1 + a 2 x

Passo 2

A segunda função, é dada por...

y 2 = 1 a + b x

Com base em uma variável auxiliar z 2 , linearizando, ficamos com...

z 1 = 1 y 2 = a ⏟ b 1 + b ⏟ b 2 x = b 1 + b 2 x

Passo 3

Já a terceira função vem com a seguinte cara...

y 3 = x a + b x

Linearizando com uma variável auxiliar z 3 :

z 3 = 1 y 3 = a + b x x = b ⏟ c 1 + a ⏟ c 2 1 x

Chamando 1 x de x 3 , então temos que...

z 3 = c 1 + c 2 x 3

Então, chegamos até os resultados da seguinte tabela abaixo...

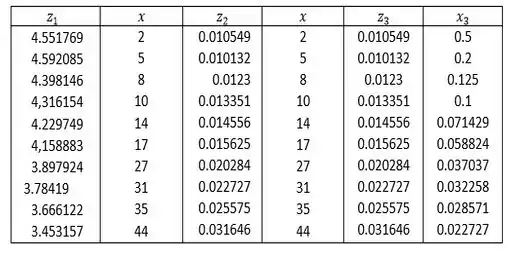
Tá legal! Agora vamos aos gráficos...

Esse é o gráfico da função y = x / ( a x + b ) ...

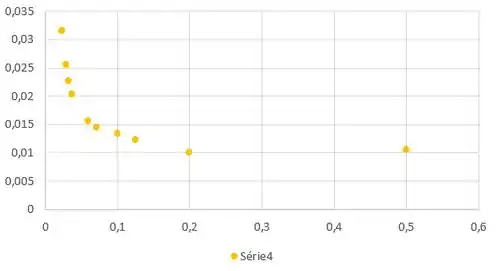
Este é o gráfico da função y = 1 / ( a x + b ) :

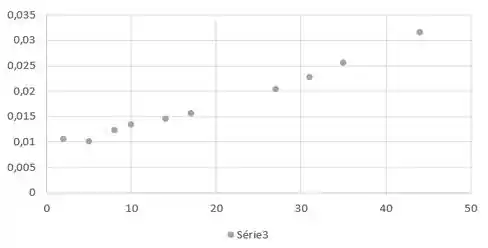
E este é o gráfico da função y = a e b x :

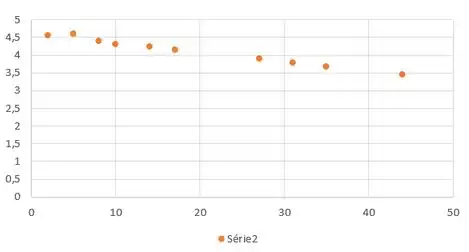
Logo, como podemos ver, os pontos estão mais linearizados em y = a e b x . Logo, é com essa função que vamos aproximar!

Passo 4

Agora que já sabemos que a curva escolhida é...

y = a x b

Pela tabela, obtemos que...

a = 95.9474

b = - 0.0249

Sendo assim...

y = 95.9474 ⋅ e - 0.0249 x

E o resíduo minimizado foi de 1 / y como função de x .

Resposta

a)

y = a e b x

b)

a = 95.9474

b = - 0.0249

y = 95.9474 ⋅ e - 0.0249 x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dada a tabela abaixo, faça o gráfico de dispersão dos dados e ajuste uma curva da melhor maneira possível:
Determinar aproximação trigonométrica de ordem 2 , em [ - π , π ] , para y ( t )= | sin ⁡ t | .
Obter aproximação trigonométrica, de ordem 1 , para a função:
Deseja-se aproximar uma função f0 tabelada por uma função do tipo: x 2 ln ⁡ ( a x 4 + b x 2 + c ) usando o método dos mínimos quadrados.a) Podemos aproximar f diretamente pela função acima? Caso não s