1. O método de Euler modificado é deduzido a partir da figura abaixo: y ( x ) : solução exata da equação diferencial L 1 : z 1 ( x ) ; reta que passa por ( y n , x n ) e é tangente a y ( x ) em ( x n , y n ) L 2 : z 2 ( x ) ; reta que tem inclinação f ( P ) L 3 : z ( x ) ; reta que passa por ( x n , y n ) e é paralela a L 2 y n + 1 = z ( x n + h ) Deduza a expressão de y n + 1 :

y n + 1 = h 2 ⋅ y n f x n , y n + f x n + 1 , y n + h ⋅ f ( x n , y n )

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 1

1. O método de Euler modificado é deduzido a partir da figura abaixo:

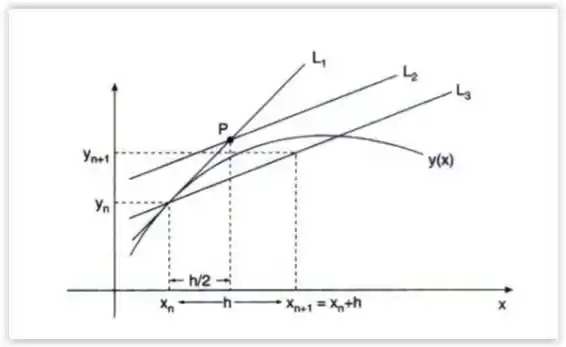
: solução exata da equação diferencial

: ; reta que passa por e é tangente a em

; reta que tem inclinação

; reta que passa por e é paralela a

Deduza a expressão de :

Passo 1

E aí galerinha! Bora deduzir aqui graficamente o método de Euler modificado!

Se liga só! Do método de Euler, a gente já sabe a seguinte fórmula:

Mas porque que a gente falou aqui do método de Euler se o que a gente quer é o aperfeiçoado...

Ow queridão! O método de Euler aperfeiçoado é apenas uma variação do método de Euler. Se um pega a reta tangente ao gráfico o outro pega a reta secante...

Passo 2

Agora pega a reta ... Chamando a inclinação dela de , temos que...

E se liga na imagem abaixo, que é um esboço do que mais ou menos a gente tá pretendendo fazer...

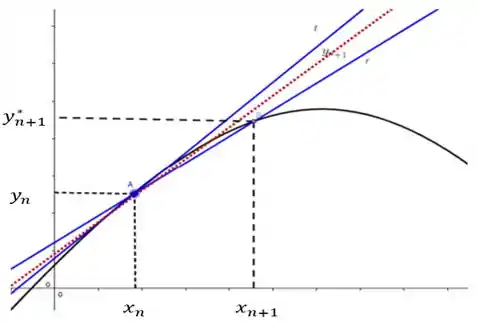
Repara em . Pelo método de Euler, temos que ele é dado por...

No método de Euler, esse vem após a primeira iteração. E assim, temos que...

Sendo assim, pegando a reta e o ponto abaixo...

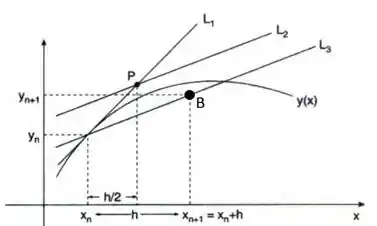
Temos que...

Sendo a inclinação da reta que passa pelo ponto , e é paralela a dada por...

E assim, temos a modificação do método, onde se faz a média entre e ...

E assim, chegamos à fórmula do Método de Euler modificado!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método de Euler com o passo especificado para calcular o valor da solução no ponto dado x*. Determine o valor da solução exata em x* y ' = x y , y0 ,y 0 = 1 d x = 0,1 x * = 1

8. Use vários métodos e vários valores de h para encontrar y ( 2 ) sendo dado o PVI: y ' = cos ⁡ x + 1 y 0 = - 1

4.a) Verifique que fazendo m = 1 e p = 1 nos métodos ( 3 ) do texto, obtemos o método y n + 1 = y n - 1 + 2 h f n com erro h 3 3 y ' ' ' ( ξ ) b) Em termos de esforço computacional como você compara c

6. a) Deduza o método implícito para resolver o PVI: y ' = f ( x , y ) y x 0 = y 0,d ot i p oy n + 1 = y n + ∫ x n x n + 1 f x , y x d x Onde usamos a regra dos Trapézios para calcular a integral acim

7. a) Considerando o seguinte PVI y ' = 0.04 y y 0 = 1000 E supondo conhecidos y 1 e y 2 , verifique que o método (2) do texto nos fornece y n + 1 explicitamente para y n + 1 .b) Como você explica o r