Em contraste com o exercício anterior, considere:

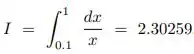
Usando a regra de Simpson sobre N intervalos obteve-se a tabela:

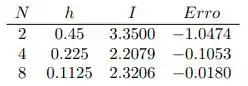
Explique a diferença entre estes resultados e os do exercício anterior.

Eaii! Tudo belezinha? Neste exercício precisaremos analisar a tabela e comparar os resultados obtidos para a integral fornecida no enunciado, com os resultados do exercício anterior (29). Vamos lembrar que no exercício 29, tínhamos um passo (h) muito alto que era 0.5 e mesmo com um passo grande assim, nosso erro era muito pequeno, o que fazia com que o valor da integral calculado pela regra de Simpson fosse extremamente próximo ao valor exato. Já neste caso, de acordo com a tabela, quando o h é alto, o erro também é muito alto, e somente com um passo muito pequeno (como 0.1125) foi obtido um erro aceitavelmente pequeno.

Basicamente, analisamos e comparamos os resultados da tabela, com o resultado do exercício anterior. Era isso! Valeu! Até o próximo!