Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 16

16. Considere o PVI

Passo 1

a) Calcule aproximações para y ( 1 ) usando o método de Euler com h = 0.2 e h = 0.25

b) Repita o item (a), usando agora o método de Euler aperfeiçoado.

Passo 2

a) E aí meus caros e caras!

Se liga só! O PVI do exercício 16 é dado por...

Passo 3

E temos que resolver ele usando diferentes valores de h . O que nós temos que fazer aqui é achar o y ( 1.0 ) ... Por isso, conforme pede a questão, vamos recorrer aos métodos de Euler e Euler modificado

Passo 4

Chamando então y ' de f ( x_n , y_n ) , temos para o método de Euler, a seguinte fórmula de recorrência...

y_n + 1 = y_n + h f ( x_n , y_n )

y_n + 1 = y_n + h ((y_n^2 - 1)/(x_n^2 + 1))

y_n + 1 = y_n + h ((y_n^2 - 1)/(n^2 h^2 + 1))

E fazendo um código em linguagem C para isso, chegamos ao exposto na seguinte imagem abaixo, para h = 0.2 ;

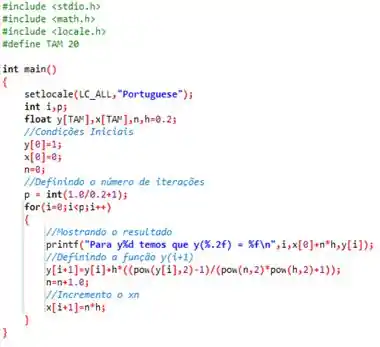
Compilando ele, para os valores de h pedidos, obtemos que para h = 0.2 ...

y (1) = 1.0

E para h = 0.25 ;

y (1) = 1.0

Passo 5

b) Usando dessa vez, Euler melhorado, temos que a fórmula de recorrência vai ser dada por...

y_n + 1 = y_n + (h)/(2) [ f (x_n , y_n) + f ( x_n + 1 , y_n + 1 ) ]

y_n + 1 = y_n + (h)/(2) [(y_n^2 - 1)/(n^2 h^2 + 1) + (y_(n + 1)^2 - 1)/(x_(n + 1)^2 + 1)]

y_n + 1 = y_n + (h)/(2) [(y_n^2 - 1)/(n^2 h^2 + 1) + (k_n^2 - 1)/(( n + 1 )^2 h^2 + 1)]

Sendo que k_n é dado por...

k_n = y_n + h ((y_n^2 - 1)/(n^2 h^2 + 1))

Desse modo, dando uma leve modificada no código anterior, obtemos para h = 0.2 ...

y (1) = 1.0

E para h = 0.25 ;

y (1) = 1.0

Resposta

a)

P a r a h = 0.2 e 0.25 -> y (1) = 1.00000

b)

P a r a h = 0.2 e 0.25 -> y (1) = 1.00000

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o .a) Encontre a solução aproximada usando o método de Euler com h = 0.5 eh• 0.25, considerando x E [O, 2]; b) idem, usando Euler Aperfeiçoado; c) idem, usando Runge-Kutta de 41 ordem; d) sa
3. Dado o PVI abaixo, considere h = 0.5, 0.25, 0.125 e 0.1 y ' = 4 - 2 x y 0 = 2 a) Encontre uma aproximação para y ( 5 ) usando o método de Euler aperfeiçoado, para cada h .b) Compare seus resultados
21. Considere o PVI
19. Considere o problema: y ' ' + 7 y = 0 y 0 = 2 y ' 0 = 0 Com x ∈ [ 0 ,1 ] a) reescreva os métodos de Euler e Euler aperfeiçoado para resolver este problema como um sistema de equações de 1ª ordem;b