Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 3
3. Dado o PVI abaixo, considere h = 0.5, 0.25, 0.125 e 0.1
a) Encontre uma aproximação para usando o método de Euler aperfeiçoado, para cada .
b) Compare seus resultados com a solução exata dada por . Justifique.
c) Você esperava o mesmo resultado do item (b) usando o método de Euler? Justifique.
Passo 1
a) E aí meus queridossss!
Se liga só! Vamos usar o método de Euler aperfeiçoado pra resolver essa primeira letra do probleminha!
Bora chamar o de . Com isso, temos que...
E usando a fórmula de recorrência do método de Euler, temos que...
Passo 2
Pois muito bem! A questão pede pra gente determinar o valor de
E é aí que tá o problema! Não tem outro jeito da gente fazer isso se não for computacionalmente!
Sabe o porquê!
Se liga só no tanto de iteração que ia nos custar pra fazer isso aqui com um passo de ...
Isso com !
Então bora recorrer a programação!
Passo 3
Se liga só! O algoritmo do método de Euler aperfeiçoado é bem simples...
Calma que o produtor vai dar o passo a passo direitinho dele aqui...
: Dados iniciais (o que seu programa vai receber de você; bibliotecas, constantes, etc.)
Passo
b) Intervalo em que vamos estimar ,
c) Valor inicial
: Define-se um vetor onde vamos guardar as estimativas de , de modo que
: Define-se um vetor formado pelos pontos onde vamos estimar as derivadas
Define-se
: Para de até repita os passos e
:
:
Passo 4
Sendo assim, com base nos procedimentos demonstrados anteriormente...
O seguinte código abaixo foi confeccionado em linguagem ...
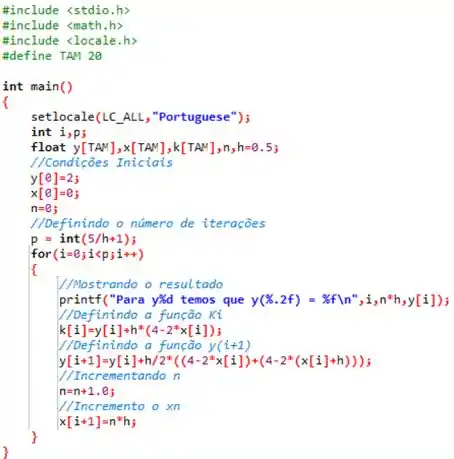
O legal de fazer um código é que pra achar o valor de nos outros passos e , basta mudar o valor de . Sendo assim, compilando o código para os diferentes valores de, obtemos os seguintes valores:
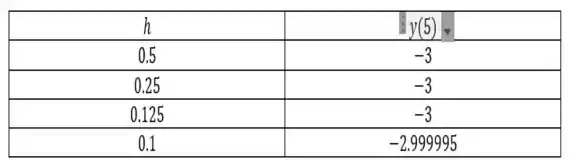
Passo 5
b) Sabemos que a solução exata é dada por...
Pois muito bem! Vamos ver qual o valor de quando ...
Fazendo isso, obtemos que:
Ou seja! É um valor bem próximo dos que a gente obteve quando usou o método de Euler modificado!
Passo 6
c) Agora, vamos ver como ficaria com o método de Euler
O algoritmo do método de Euler é bem de boas! É até mais simples do que o do método de Euler modificado, como podemos ver abaixo...
: Dados iniciais (o que seu programa vai receber de você; bibliotecas, constantes, etc.)
Passo
b) Intervalo em que vamos estimar ,
c) Valor inicial
: Define-se um vetor onde vamos guardar as estimativas de , de modo que
: Define-se um vetor formado pelos pontos onde vamos estimar as derivadas
Define-se
: Para de até repita o passos
:
E o nosso código fica assim...
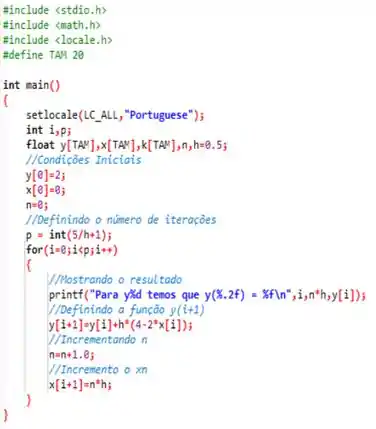
E obtemos assim, os seguintes resultados...
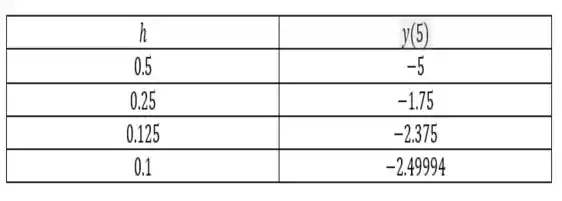
Que são um pouco mais divergentes dos resultado do item (a) e do real resultado da letra (b).
E isso não é uma surpresa, né galera? Afinal, o método de Euler aperfeiçoado, como o próprio nome diz, fornece uma solução mais próxima do valor exato, já que sua equação está relacionada à reta secante e não à reta tangente.
Resposta
a)
b)
c)