Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 19

19. Considere o problema:

y ' ' + 7 y = 0 y 0 = 2 y ' 0 = 0

Com x ∈ [ 0 ,   1 ]

a) reescreva os métodos de Euler e Euler aperfeiçoado para resolver este problema como um sistema de equações de 1ª ordem;

b) resolva o problema usando Euler aperfeiçoado e h = 0.25

Passo 1

a) E aí meus queridos!

Manos e Manas! Se liga só! O PVI do exercício 19 é dado por...

y ' ' + 7 y = 0 y 0 = 2 y ' 0 = 0

E o que a questão pede pra gente inicialmente, é reescrever ele usando os método de Euler e Euler aperfeiçoado.

Passo 2

Chamando então y ' de z e y de w temos que o P V I de antes vai ficar assim...

z ' + 7 w = 0 w 0 = 2 z 0 = 0

Então, chamando z ' de f ( x n , y n ) , temos que para o método de Euler, vamos ficar com a seguinte fórmula...

f x n , y n , w n = - 7 w n

Com...

y 0 = w 0 = 2

Desse modo, temos que...

y n + 1 = y n + h f ( x n , y n , w n )

y n + 1 = y n - 7 h w n

y n + 1 = w n - 7 h w n

Passo 3

Já para o método de Euler aperfeiçoado, temos que...

y n + 1 = y n + h 2 f x n , y n , w n + f x n + 1 , y n + 1 , w n + 1

y n + 1 = y 0 + h 2 ( - 7 w n - 7 w n + 1 )

Passo 4

b) Baseado nisso, utilizando o método de Euler com h = 0.25 e x variando de 0.25 até 1 , obtemos os resultados da tabela abaixo...

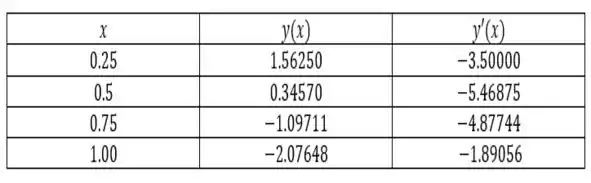
Resposta

a)

y n + 1 = w n - 7 h w n

y n + 1 = y 0 + h 2 ( - 7 w n - 7 w n + 1 )

b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16. Considere o PVI
Considere o .a) Encontre a solução aproximada usando o método de Euler com h = 0.5 eh• 0.25, considerando x E [O, 2]; b) idem, usando Euler Aperfeiçoado; c) idem, usando Runge-Kutta de 41 ordem; d) sa
3. Dado o PVI abaixo, considere h = 0.5, 0.25, 0.125 e 0.1 y ' = 4 - 2 x y 0 = 2 a) Encontre uma aproximação para y ( 5 ) usando o método de Euler aperfeiçoado, para cada h .b) Compare seus resultados
21. Considere o PVI