Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 17

Considere o

.

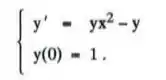a) Encontre a solução aproximada usando o método de Euler com h = 0.5 eh• 0.25, considerando x E [O, 2];

b) idem, usando Euler Aperfeiçoado;

c) idem, usando Runge-Kutta de 41 ordem;

d) sabendo que a solução analítica do problema é y - exp(-x + x3 /3), coloque num mesmo gráfico a solução analítica e as soluções numéricas encontradas nos itens anteriores. Compare seus resultados.

Passo 1

Vamos usar Euler com a seguinte configurações:

f ( t , y ) = y t 2 - y

y 0 = 1

h = 0.5   e h = 0.25

A fórmula de recorrência fica:

y n + 1 = y n + h ( y n n 2 h 2 - y n )

Passo 2

para h   =   0.5 :

y ( 0 ) = 1

y ( 0.5 ) = 0.5

y ( 1 ) = 0.3125

y ( 1.5 ) = 0.3125

y ( 2 ) = 0.507813

Passo 3

para h = 0.25 :

y ( 0 ) = 1

y ( 0.25 ) = 0.75

y ( 0.5 ) = 0.574219

y ( 0.75 ) = 0.466553

y ( 1 ) = 0.415524

y ( 1.25 ) = 0.415524

y ( 1.5 ) = 0.473957

y ( 1.75 ) = 0.62207

y ( 2 ) = 0.94282

Passo 4

A tabela geral para h=0,25 será:

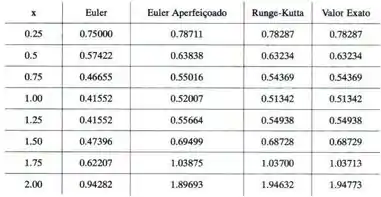
Já para h=0,5:

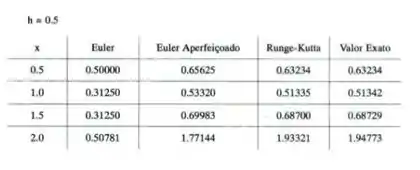
Resposta

Para h = 0.25 ,   y ( 2 ) = 0.94282

Para h = 0.5 ,   y ( 2 ) = 0.507813

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16. Considere o PVI
3. Dado o PVI abaixo, considere h = 0.5, 0.25, 0.125 e 0.1 y ' = 4 - 2 x y 0 = 2 a) Encontre uma aproximação para y ( 5 ) usando o método de Euler aperfeiçoado, para cada h .b) Compare seus resultados
21. Considere o PVI
19. Considere o problema: y ' ' + 7 y = 0 y 0 = 2 y ' 0 = 0 Com x ∈ [ 0 ,1 ] a) reescreva os métodos de Euler e Euler aperfeiçoado para resolver este problema como um sistema de equações de 1ª ordem;b