Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios complementares - Ex. 26II

Calcule as integrais a seguir pela regra do trapézio e pelas regras 1 3 𝑒   3 8 de Simpson usando 6 divisões do intervalo de integração. Compare os resultados.

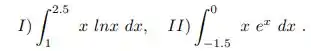
Passo 1

Eai, tudo belezinha? Agora vamos para o item II.Teremos que usar a regra do trapézio, 1 3 𝑒   3 8 para resolver a mesma integral. Sabendo que teremos 6 intervalos, ficaremos com as seguintes fórmulas compostas:

Trapézio:

h 2 𝑦 0 + 2 𝑦 1 + 2 𝑦 2 + 2 𝑦 3 + 2 𝑦 4 + 2 𝑦 5 + 𝑦 6

1 3

De Simpson:

h 3 𝑦 0 + 4 𝑦 1 + 2 𝑦 2 + 4 𝑦 3 + 2 𝑦 4 + 4 𝑦 5 + 𝑦 6

3 8

De Simpson:

3 h 8 𝑦 0 + 3 𝑦 1 + 3 𝑦 2 + 2 𝑦 3 + 3 𝑦 4 + 3 𝑦 5 + 𝑦 6

Passo 2

Considerando que o passo h será 0 − − 1.5 6 = 0.25 , nosso intervalo de pontos será o seguinte:

− 1.5 , − 1.25 , − 1.0 , − 0.75 , − 0.5 , − 0.25,0  

Agora só precisamos substituir os valores nas fórmulas:

Trapézio:

0.25 2 − 1.5 𝑒 − 1.5 + 2 − 1.25 𝑒 − 1.25 + … + 2 − 0.25 𝑒 − 0.25 + 0 𝑒 0 = − 0.43639

1 3 Simpson:

0.25 3 − 1.5 𝑒 − 1.5 + 4 − 1.25 𝑒 − 1.25 + … + 4 − 0.25 𝑒 − 0.25 + 0 𝑒 0 = − 0.44211

3 8 Simpson:

3 0.25 8 − 1.5 𝑒 − 1.5 + 3 − 1.25 𝑒 − 1.25 + … + 3 − 0.25 𝑒 − 0.25 + 0 𝑒 0 = − 0.44204

E com isso resolvemos a integral utilizando os 3 métodos. Note que tivemos mais casas decimais corretas nas regras 1 3 e 3 8 de Simpson, assim como no item I do mesmo exercício. Acabamos! Até mais.

Resposta

Trapézio = − 0.43639   .

1 3 de Simpson = − 0.44211   .

3 8 de Simpson = − 0.44204   .

Exercícios de Livros Relacionados

Resolver os exercícios 11.1, 11.2, 11.3, 11.4 usando a Regra 1 3 de Simpson.
Usando a regra 3 8 de Simpson e h=0.6, 0.2, calcular:Sabe-se que:
Calcular:Pela regra 3 8 de Simpson; com h=0.1 . Use a tabela do exercício 11.2 .
Resolver os exercícios 11.1 e 11.8 usando a regra 3 8 de Simpson.
Resolver os exercícios 11.1, 11.2, 11.3, 11.4 usando a Regra 1 3 de Simpson.