Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios - Ex. 4

Dada a tabela:

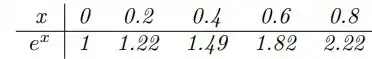
Calcular:

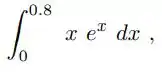
Pela regra do trapézio usando todos os pontos.

Passo 1

Eaí, tudo beleza? Vamos utilizar a regra do trapézio para calcular a integral. A fórmula básica é a seguinte:

h 2 𝑦 0 + 𝑦 1

Porém, como iremos considerar todos os pontos da tabela, vamos mexer na fórmula.Sabendo que o passo (h) será 0.8 − 0 4 = 0.2 , ficamos com a seguinte expressão:

0.2 2 𝑦 0 + 2 𝑦 1 + 2 𝑦 2 + 2 𝑦 3 + 𝑦 4

Passo 2

Substituindo os valores de acordo com a tabela para chegar no resultado final, não se esqueça de multiplicar 𝑒 𝑥   por 𝑥   :

0.2 2 0 1 + 2 0.2 1.22 + 2 0.4 1.49 + 2 0.6 1.82 + 0.8 2.22 = 0.564

E finalizamos por aqui! Até o próximo.

Resposta

O valor da integral foi aproximadamente 0.564   .

Exercícios de Livros Relacionados

Qual o erro máximo cometido na aproximação de ∫ 0 4 ( 3 x 3 - 3 x + 1 ) d x pela regra dos Trapézios com quatro subintervalos?
Usando as integrais do exercício anterior com quantas divisões do intervalo, no mínimo, podemos esperar obter erros menores que 1 0 - 5 ?
Em que sentido a regra de Simpson é melhor do que a regra dos Trapézios?
Calcule as integrais a seguir pela regra dos Trapézios usando quatro e seis divisões de [a,b]. ∫ 1 2 e x d x ∫ 1 4 x d x ∫ 2 14 d x x
Uma maneira de se obter numericamente valores da função 𝑓 𝑥 = l n l n𝑥 é calcular numericamente valores da integral: l n l n𝑥= ∫ 1 𝑥 𝑑 𝑡 𝑡 ,Calcular:II) l n l n   3.5