Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Exercícios complementares - Ex. 42a

Dado o sistema não linear:

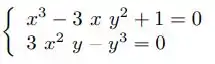
Determine uma solução com 2 dígitos significativos corretos, iniciando com ( x 0 , y 0 ) = ( 0.51,0.85 ) ; e usando:

a) método iterativo linear

Passo 1

Eaí meu colega, bora para mais um?

Vamos utilizar o método iterativo linear aplicado a sistemas de equações não lineares, buscando uma aproximação de solução. Não se assuste! Vamos fazer o mesmo esquema de sempre, transformando a equação, só teremos que tomar mais cuidado para não ter algum errinho de conta.

Bora então, começaremos criando equações iterativas para x e y.

Para a primeira equação (x), ficaremos com:

𝑥   =   3 𝑥 𝑦 2 − 1 3

Para a segunda equação (y), ficaremos com:

𝑦 = 3 𝑥 2 𝑦 3

Passo 2

Com as equações que obtemos, agora só precisamos usar os valores iniciais e aplicar o método iterativo linear:

𝑥 1   =   3 0.51 0.85 2 − 1 3 =   0.47240

𝑦 1 = 3 0.51 2 0.85 3 =   0.87208

𝑥 2   =   3 0.47240 0.87208 2 − 1 3 = 0.42692

𝑦 2 = 3 0.47240 2 0.87208 3 = 0.83579

𝑥 3   =   3 0.42692 0.83579 2 − 1 3 = − 0.47226 …

Podemos notar que não tivemos convergência para a equação iterativa escolhida... Então, iremos parar por aqui.

Resposta

Não tivemos convergência durante as iterações.

Exercícios de Livros Relacionados

Determinar, pelo método das secantes, uma raiz de cada uma das equações:a) 𝑥   =   2.7 l n l n𝑥
Calcular P(5) e P’(5) para o polinômio: 𝑃 (𝑥) = 𝑥^5 - 3 𝑥^4 + 2 𝑥^2 - 3 𝑥 + 5 .
Dado o sistema não linear:Determine uma solução com 2 dígitos significativos corretos, iniciando com (x0, y0) = (0.51, 0.85); e usando:b) método de Newton
Mostre que o sistema não linear: 3 x 2 + y 2 + 9 x - y - 12 = 0 x 2 + 36 y 2 - 36 = 0 Possui exatamente 4 raízes. Determine as raízes usando o método de Newton, com 2 dígitos significativos corretos,