Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Exercícios complementares - Ex. 38
Usando o método de Newton determine t (real), com erro relativo inferior a , tal que a matriz:
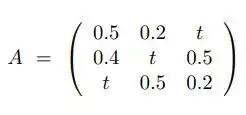
Seja singular.
Passo 1
Opaa! Tudo belezinha? Vamos resolver o exercício proposto, ok? Primeiramente precisamos encontrar uma equação em função de t, para depois poder usar o método de Newton. Para isso, vamos calcular o determinante da matriz:
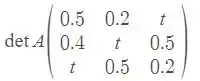
Resolvendo, chegamos em:
E com isso, iremos calcular t, pelo método de Newton. Mas antes vamos derivar, já que iremos precisar já, já:
Passo 2
Aplicando o método de Newton utilizando como valor inicial , pego graficamente:
E com isso, encontramos o valor aproximado de t! Até o próximo!
Resposta
Exercícios de Livros Relacionados
Usando alguma linguagem de programação, escreva um programa para o método de Newton e para o método de Newton Modificado.
Considere um circuito de polarização que consiste de uma bateria com uma tensão V B= 2.0V e um resistor Rd e50Ω em série, conectado a um diodo semicondutor de estado sólido como mostrado na Figura 3.2
Num escoamento turbulento em uma rede de tubulação interconectada, a razão de escoamento V de um nós. Para outro é proporcional à raiz quadrada da diferença entre as pressões nos nós. Para a rede da f
A Figura abaixo representa o fluxo de água em um canal aberto:Uma relação empírica para o fluxo é a equação de Chez-Manning: Q = 1,49 E A R 2 3 S 1 2 Onde: • Q -f l u x oe m m 3 s e g . ; • E - c o e
Muitas equações de estado foram desenvolvidas para descrever as relações entre pressão, P , volume molar, V , e temperatura, T , de gases. Uma das equações mais utilizadas é equação de Beattie-Bridgem