Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Exercícios complementares - Ex. 42b
Dado o sistema não linear:
Determine uma solução com 2 dígitos significativos corretos, iniciando com (x0, y0) = (0.51, 0.85); e usando:
b) método de Newton
Passo 1
Saaalve meu amigo(a)! Vamos repetir o esquema do item a, porém utilizando o método de Newton agora.
Para utilizar o método de Newton, precisaremos da seguinte relação:
Onde J é o jacobiano das derivadas parciais de cada equação, S é a solução e F é o valor da função aplicada a um número inicial .
Passo 2
Calculando o Jacobiano e montando segundo a relação que passei ficamos com o seguinte monstrinho:
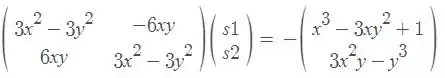
Note que na matriz do jacobiano, temos as derivadas parciais de X na primeira coluna e na segunda as de Y! Agora só precisamos realizar substituições usando os valores iniciais do enunciado, conforme o exemplo abaixo:
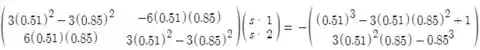
Resolvendo as iterações necessárias, chegamos em .
Resposta
.