Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios - Ex. 14

Determinar h de modo que a regra 3 8 de Simpson forneça o valor de

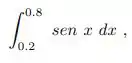
Com erro inferior a 0.5 × 10 − 3 .

Passo 1

Oie! Tudo certinho? Neste exercício, iremos analisar o erro da regra 3 8 de Simpson, que pode ser calculado de acordo com a seguinte expressão:

𝑒   =   − 3 80 h 5 𝑓 𝑖 𝑣 𝑡 ,   𝑡   ∈   𝑎 , 𝑏

Onde o intervalo   𝑎 , 𝑏 é o intervalo de integração, h é o passo (que queremos achar) e 𝑓 𝑖 𝑣 𝑡

é a quarta derivada da função aplicada no ponto do intervalo que maximiza seu valor. Com isso, podemos calcular o valor de h.

Passo 2

Sabendo que queremos um erro inferior a 0.5   × 10 − 3 , podemos fazer o seguinte:

0.5   × 10 − 3   ≥ − 3 80 h 5 𝑓 𝑖 𝑣 𝑡

Para encontrar o valor de h, será necessário, primeiramente, calcular a derivada quarta de 𝑠 𝑒 𝑛   𝑥   , que é igual a 𝑠 𝑒 𝑛   𝑥   (coincidência, não?). Agora vamos testar qual ponto do intervalo maximiza seu valor:

𝑠 𝑒 𝑛 0.2 = 0.1986 …   𝑒   𝑠 𝑒 𝑛 0.8 = 0.7173 ...

Logo, achamos o valor da derivada quarta da função, maximizado, que é 0.7173   .

Com isso, ficamos com:

0.5 ×   10 − 3 ≥ − 3 80 h 5 0.7173

Efetuando os cálculos a gente encontra que, em módulo, h   ≅   0.45   para que o erro desejado seja atingido.

Resposta

h   ≅   0.45   .

Exercícios de Livros Relacionados

Calcule as integrais impróprias.
Use a regra de Simpson para aproximar o valor médio da temperatura da função f x = 37s e n 27 365 x - 101 + 25 Para um ano de 365 dias. Essa é uma forma de estimar a temperatura média anual do ar em F
O calor especifico de um gás C é a quantidade de calor necessária para elevar a temperatura em 1° C de determinada massa de gás com volume constante, medida em Cal/°C-mol (calorias por grau centígrado
U se a regra do Trapézio para fazer uma aproximação do consumo de combustível total durante aquela hora. Se o automóvel fez 60 milhas nessa hora, qual foi a eficiência do combustível (em milhas por ga
De acordo com a fórmula que limita o erro para a regra de Simpson, quantos subintervalos você deve usar área estimar o valor de l n 3 = ∫ 1 1 1 xd x Pela regra de Simpson com um erro de não mais que 1