Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios - Ex. 13

Achar o número mínimo de intervalos que se pode usar para, utilizando a regra 1 3 de Simpson obter:

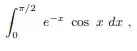
Com 4 casas decimais corretas.

Passo 1

Opa!! Semelhantemente ao exercício anterior, iremos usar as fórmulas de erros dos métodos de integração numérica. Para ser mais específico, usaremos o erro para o método 1 3 de Simpson, dado por:

𝑒 = − 𝑛 90 𝑓 𝑖 𝑣 𝑡 h 5 ,   𝑡   ∈   𝑎 , 𝑏

Onde 𝑓 𝑖 𝑣 𝑡 é a derivada quarta aplicada no ponto do intervalo que maximiza seu valor, 𝑛   é o número de intervalos e h   é o passo.Outra forma de calcular o erro (que é equivalente à de cima) é:

𝑒   =   − h 4 𝑏 − 𝑎 180 𝑓 𝑖 𝑣 𝑡

Se encontrarmos h, poderemos achar 𝑛   , sabendo que h = 𝑏 − 𝑎 𝑛 .

Passo 2

Calculando a derivada quarta de 𝑒 − 𝑥 c o s c o s   𝑥   , chegamos em:

− 4 𝑒 − 𝑥 c o s c o s   𝑥  

E substituindo x por zero ou 𝜋 2 , descobrimos que seu valor é maximizado quando x = 0 com valor de :

𝑓 𝑖 𝑣 0 = − 4

Agora vamos substituir na expressão considerando que queremos um erro menor que 10 − 4 :

10 − 4 ≥ − h 4 𝜋 2 180 − 4

E com isso calculando essa conta linda, concluímos que:

h 4 ≤ 9 1000 𝜋

h ≤ 0.23 …  

Agora usando h para encontrar 𝑛   :

h = 𝑏 − 𝑎 𝑛

𝑛 = 𝑏 − 𝑎 h

𝑛 = 𝜋 2 0.23 … ≈ 7

Para um erro igual a 10 − 4 seriam necessários 7 intervalos, porém, como consideramos números pares de intervalos na regra 1 3 de Simpson, tomaremos 𝑛   =   8   . Acabamos, até mais!

Resposta

𝑛   =   8   .

Exercícios de Livros Relacionados

Você planeja usar a regra de Simpson para estimar o valor da integral ∫ 1 2f x d x Com uma magnitude de erro inferior a 10 - 5 . Você determinou que f 4 x ≤ 3 ao longo do intervalo de integração . Qua
Um breve cálculo demonstra que se 0 ≤ x ≤ 1 , então a segunda derivada de f x = 1 + x 2 fica entre 0 e 8 . Com base nisso, diga quantas subdivisões serão necessárias, aproximadamente, para estimar a i
Para atender à demanda por vagas, sua cidade alocou a área mostrada a seguir . Como você é o engenheiro da cidade, a câmera lhe pediu para determinar se é possível construir o estacionamento com $ 11.
Um cálculo direto mostra que. ∫ 0 π2s e n 2 xd x = π Quão próximo desse valor você chega usando a regra do trapézio com n = 6? E a regra de Simpson com n = 6 ? Experimente e descubra.
111. Dada a integral ∫ d d + 6 x 2 + b x + c d x , onde b, c e d são constantes. Suponha que essa integral seja aproximada pela regra do trapézio com n = k . (a) Mostre que o erro na aproximação é ext