Enunciado
Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.6 - Ex. 29
Prove que a soma na regra do trapézio para é uma soma de Riemann para contínua em . Dica: use o teorema do valor intermediário para mostrar a existência de no subintervalo que satisfaz:
Passo 1
Em exercícios anteriores já trabalhamos a regra do trapézio, mas se você se esqueceu, não se preocupa, vou relembrar rapidinho.
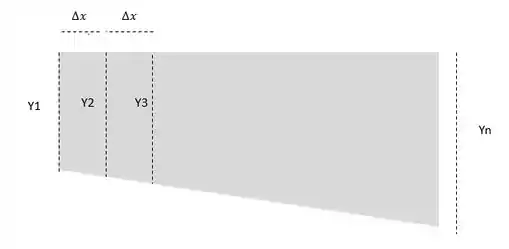
Vamos calcular a área dessa figura dividindo em vários trapézios pequenos. A área total é a soma das áreas deles!
Está vendo que podemos agrupar essa soma? Então vamos arrumar isso!
E pronto, essa é a forma geral do método dos trapézios. Vamos substituir os nossos valores, lembrando que .
Passo 2
Uma soma de Riemann consiste em aproximar uma curva por retângulos, porque conhecemos bem a área deles!
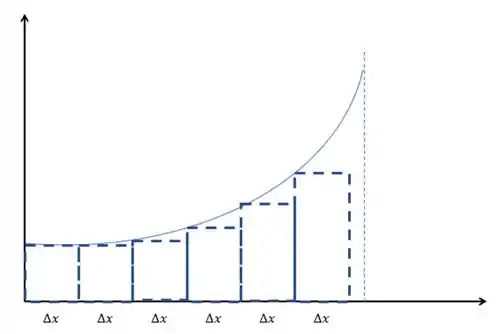
Quanto mais fininhos os retângulos, mais adequada vai ser a aproximação! A área vai ser, aproximadamente:
Percebeu? Nas duas a gente usou basicamente a mesma idéia! A aproximação por trapézios é só uma derivação da aproximação por retângulos de Riemman. De qualquer forma, ao escolhermos cada vez menores, ou seja, limites de tendendo a , o somatório nos dois casos vira uma integral!
Resposta
Ei, a resposta está no passo a passo :)