Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.6 - Ex. 34

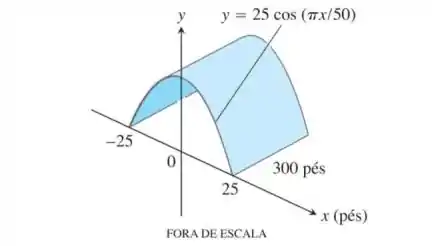
Sua empresa de engenharia está tentando fechar contrato para a construção de um túnel, como o que mostra a figura a seguir. O túnel tem 300   p é s de comprimento por 50   p é s de largura na base. Sua seção transversal tem a forma de um arco da curva y   =   25   c o s   ( π x / 50 ) . Após a conclusão, a superfície interna do túnel (excluindo a pista) será tratada com um selante impermeável cuja aplicação custa $   1,75 por pé quadrado. Quanto custará a aplicação do selante? (Dica: use integração numérica para calcular o comprimento da cossenoide.)

Passo 1

Aviso aos Navegantes: Essa é uma questão de integração numérica. Isso significa que precisaremos de uma calculadora em algum momento de nosso cálculo. Então nós queremos saber na real o comprimento da função 25   c o s   ( π x / 50 ) . E depois multiplicar por 300 * 1,75 , para obter o custo total.

Vamos lembrar que o comprimento (   C   ) de uma função pode ser encontrada por :

C =   ∫ a b 1 + f ' x 2     d x

Então precisamos encontrar a derivada de nossa função primeiro.

Passo 2

f x =   25   c o s   ( π x / 50 ) .    

f ' x = - 25 * π 50 s e n π x / 50    

f ' x 2 = π 2 4 sen 2 ⁡ π x / 50  

Então nosso comprimento fica

C =   ∫ a b 1 + f ' x 2     d x

C =   ∫ - 25 25 1 + π 2 4 sen 2 ⁡ π x / 50       d x

E é essa a parte numérica. Vamos apelar para nossa calculadora.

C = 73,2   p e

Agora vamos calcular o custo total (   C T )

C T = 73,2 * 300 * 1,75 → R $   38.430

Por aqui terminamos, te encontro na próxima resolução. : )

Resposta

C T = R $   38.430

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9. Obtenha a fórmula do Erro para a regra dos Trapézios e para a regra de 1/3 de Simpson a partir do Teorema 1
10. Seja o problema:Interpolar a função s e n ( x ) sobre [ 0 , π 4 ] usando um polinômio de grau 2 e integrar a função neste intervalo, usando a regra de 1 3 de Simpson.Qual deve ser o menor número d
13. Dada a tabela:E sabendo que a regra de 1 / 3 de Simpson é, em geral mais precisa que a regra dos Trapézios, qual seria o modo mais adequado de calcular I = ∫ 0 1 f x d x , usando a tabela acima? A
14. Calcule pela regra dos trapézios e de Simpson cada uma das integrais abaixo, com erro menor do que ε dado:a) ∫ 0 π e s e n ( x ) d x ;ε = 2 ⋅ 10 - 2 b) ∫ 1 π 2 sen ⁡ x 1 2 d x ;ε = 10 - 4
16. Calcule π da relação π / 4 = ∫ 0 1 d x / ( 1 + x 2 ) com erro de 10 - 3 por Simpson.