Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 4.Exercícios - Ex. 2.e
Resolva os sistemas não lineares abaixo usando seus programas pata os métodos de Newton e Newton Modificado com e = 1 o-4:
Passo 1
Então, pessoal, vamos utilizar o programa desenvolvido na questão 1 para chegar nessa resposta!
Passo 2
Aqui está o código:
Passo 3
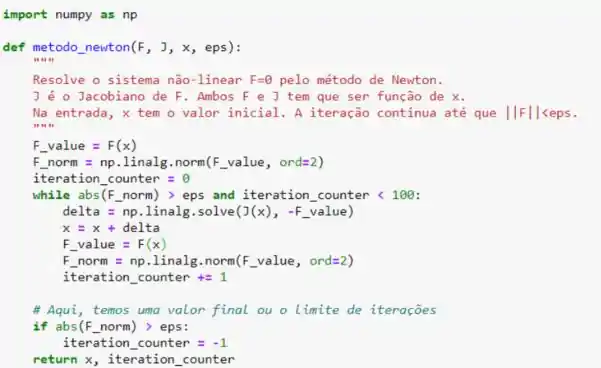
Vamos usar os seguintes valores para o Jacobiano e as funções:
Obtendo as funções
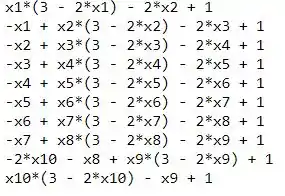
Agora para o Jacobiano:
Obtendo: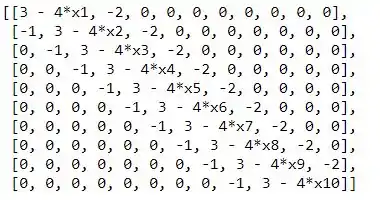
Passo 4
Utilizando o , podemos chegar ao valor de
Resposta
Exercícios de Livros Relacionados
Considere a matriz: A = 1 - 2 0 0 t 2 8 0 0 0 0 t 2 0 0 2 t Sabendo que o determinante de A é o polinômio p t = 2 t 4 - 32 , determine todos os valores de t , com erro inferior a 10 - 3 , que tornem a
Dado que: x 2 - 3,9x + 4,8 é um fator aproximado de x 4 - 4 x 3 + 4 x 2 + 4 x - 5 = 0 , use o método de Newton-Bairstow para melhorar a aproximação.
Usando o algoritmo Q - D versão Newton (para a raiz real) e Newton-Bairstow (para as raízes complexas), determine todos os zeros de P x = x 3 - x 2 + 2 x - 2 , com 4 casas decimais corretas.
A solução da equação diferencial: a n d n u ( t ) d t n + a n - 1 d n - 1 u ( t ) d t n - 1 + … + a 1 d u t d t = 0 u t = ∑ k = 1 m q k t e λ k t onde os λ k são as raízes distintas do polinômio: P λ
Seja x - uma raiz da equação f x = 0 . Supomos que f x ,f ' xe f ' ' ( x ) sejam contínuas e limitadas num intervalo fechado I contendo x = x - e que f ' x - = 0 e f ' ' x - ≠ 0 . a) mostre que o méto