Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 8

8. Use vários métodos e vários valores de h para encontrar y ( 2 ) sendo dado o PVI:

y ' = cos ⁡ x + 1 y 0 = - 1                    

Passo 1

E aí meus queridossss! Se liga só! Nessa questão, vamos usar dois métodos pra achar o y ( 2 ) , o método de Euler e o método de Euler melhorado...

Para o nosso PVI do enunciado, chamando y ' de f ( x n , y n ) ...

y ' = cos ⁡ x + 1

f ( x n , y n ) = cos ⁡ x n + 1

Sabemos que a fórmula de recorrência do método de Euler é dada por...

y n + 1 = y n + h f ( x n , y n )

E sabendo que x n é dado por...

x n = x 0 + n h = 0 + n h

x n = n h

Então, temos que...

y n + 1 = y n + h f ( x n , y n )

y n + 1 = y n + h cos ⁡ x n + 1

y n + 1 = y n + h cos ⁡ n h + 1

Passo 2

A fórmula de recorrência do método de Euler melhorado, por sua vez, é dada por...

y n + 1 = y n + h 2 [ f x n , y n + f x n + 1 , y n + h f x n , y n

y n + 1 = y n + h 2 cos ⁡ n h + 1 + cos ⁡ n + 1 h + 1

Passo 3

Agora se liga! O melhor jeito da gente resolver essa questão, é através da programação. Sabe o porquê! Se liga só no tanto de iteração que ia nos custar pra fazer isso aqui com um passo de 0.5   ...

n ú m e r o   d e   i t e r a ç õ e s = x f i n a l - x 0 h = 2 - 0 0.5 = 4

É muitos passos pra se fazer! Então bora recorrer a programação!

Passo 4

Utilizando o algoritmo que já conhecemos para os métodos de Euler, chegamos ao exposto na seguinte imagem abaixo:

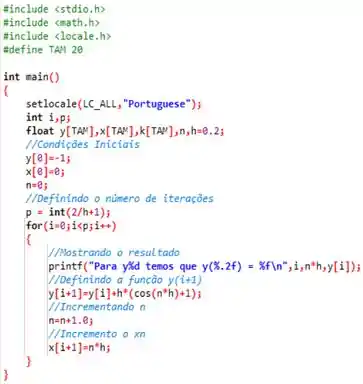
Passo 5

Já em relação ao método de Euler modificado, basta fazer algumas pequenas alterações...

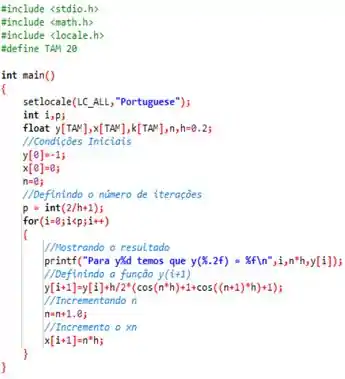
Passo 6

Dessa forma, compilando os dois códigos apenas alterando os valores de h , obtemos os resultados mostrados na seguinte tabela abaixo:

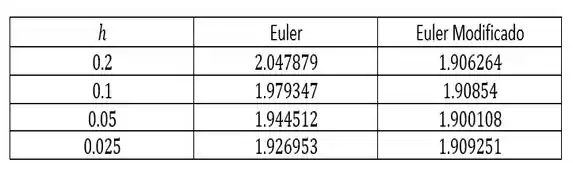
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método de Euler para resolver o problema de valor inicial no intervalo dado, começando em x 0 com d x = 0,1 . y ' = y + cos ⁡ x, y 0 = 0 ;0 ≤ x ≤ 2 ;x 0 = 0
Use o método de Euler com o passo especificado para calcular o valor da solução no ponto dado x*. Determine o valor da solução exata em x* y ' = 1 + y ² , y0 ,y 0 = 0 ² d x = 0,1 x * = 1
Use o método de Euler com o passo especificado para calcular o valor da solução no ponto dado x*. Determine o valor da solução exata em x* y ' = x y , y0 ,y 0 = 1 d x = 0,1 x * = 1
4.a) Verifique que fazendo m = 1 e p = 1 nos métodos ( 3 ) do texto, obtemos o método y n + 1 = y n - 1 + 2 h f n com erro h 3 3 y ' ' ' ( ξ ) b) Em termos de esforço computacional como você compara c