Método de Newton
Teoria
Introdução
Nós nos acostumamos ao longo da nossa vida acadêmica a trabalhar com sistemas de equações lineares. Isso porque eles têm uma série de propriedades que facilitam muito nossas contas (e vidas :P). O problema é que no mundo real os processos, de forma geral, não ocorrem de forma linear!
Assim, quando estamos solucionando um problema prático, tentamos fazer aproximações de um modelo real para que este se comporte de maneira linear. No entanto, muitas vezes isso não é possível e acabamos tendo que resolver um sistema de equações não lineares.
Mas afinal que diabos é um sistema não linear? É simplesmente um sistema onde as equações não são retas! Por exemplo:
Graficamente:
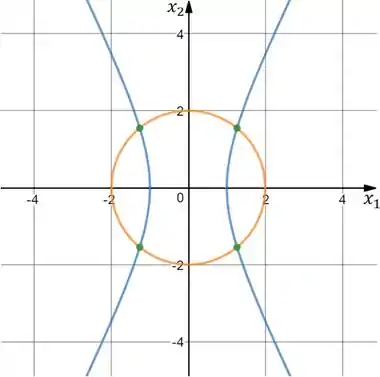
Nesse caso, como podemos ver, temos soluções, onde as equações se encontram!
E pra resolver problemas desse tipo nós vamos ver métodos iterativos para a solução de sistemas não lineares. Mas antes, precisamos de um pouco de base teórica.
Primeira coisa, vamos resolver problemas do tipo . Assim oh:
E vamos usar essa notação aqui:
Onde cada função é uma função não linear. Repare que no caso de sistemas lineares temos .
Agora nós vamos definir o vetor gradiente de denotado por :
E pra definir isso temos que assumir alguns detalhes chatos tipo que está definida em um conjunto aberto e que tem derivadas contínuas nesse conjunto (é aquele tipo de coisa que muito provavelmente nunca vai interferir em algum exercício, mas temos que mencionar assim mesmo haha).
E ainda vamos que supor que existe pelo menos um ponto , tal que (na linguagem dos mortais, estamos assumindo que o sistema tem solução).
Aí a gente acha a matriz Jacobiana definida assim:
No nosso exemplo temos:
Logo,
E é isso aí! Agora que aprendemos esses conceitos vamos ver como funciona um método desses na prática.
Método de Newton
Então, o método de Newton é o método que é mais usado para resolver sistemas de equações não lineares (é isso aí, se não tem o nome de Gauss vai ter o de Newton, parece que eles competiam haha).
Então, sem mais delongas, o que vamos fazer é o seguinte. Como todo método iterativo, nosso método de Newton vai precisar de um chute inicial . Nós vamos aplicar esse chute inicial na nossa matriz Jacobiana e na nossa e depois vamos resolver o sistema:
Aí o nosso vai ser obtido:
De forma geral, é dado por:
onde é solução do sistema:
Vamos ver um exemplo. Resolva o sistema não linear tal que:
Usando como aproximação inicial e
Passo 1: Encontramos a matriz Jacobiana.
Passo 2: Calculamos e :
Passo 3: Resolvemos o sistema :
Calculando isso aí você vai encontrar:
Então,
Passo 4: Critério de Parada
Opa, chegamos numa parte importantíssima que eu não tinha comentado ainda.
Tem dois critérios de parada principais usados nesse método. Eles são, dado um erro :
ou,
Se a questão não impuser nenhum critério você pode usar um desses, ou usar os dois juntos se quiser. Então:
Passo 5: Calculamos e :
Passo 6: Resolvemos o sistema :
Calculando isso aí você vai encontrar:
Então,
Passo 7: Critério de Parada
Que beleza, achamos o resultado exato! Então paramos por aqui!
Já deu pra pegar o espírito da coisa né? O bom de métodos iterativos é que não tem nenhuma surpresa, é sempre repetição!
Vamos dar uma olhada agora no algoritmo.
Algoritmo
Passo 1. Dados iniciais (o que seu programa vai receber de você):
a. Vetor aproximação inicial
b. Erro
Passo 2. Definimos um contador de iterações
Passo 3. Definimos a variável como o número de elementos em
Passo 4. Calcule e onde para
Passo 5. Resolva o sistema linear ,
Passo 6.
Passo 7. Se então retornar e FIM. Caso contrário,
Passo 8.
Passo 9. Para variando de a , defina
Passo 10. Se , FIM e retorne . Caso contrário, continue para o Passo 5
Passo 11.
Passo 12. Para variando de a , defina
Passo 13. Volte para o passo 3
Repare que nesse algoritmo o único critério de parada usado é a diferença . Se você quiser pode adicionar o outro critério que comentamos aqui no capítulo também. Outro critério interessante é estipularmos um número máximo de iterações como em todos os outros métodos iterativos.
Observações
Então galera, aqui vão algumas observações interessantes sobre o método de Newton!
Primeiro que para garantir a convergência precisamos de uma aproximação inicial próxima da solução do sistema. Quanto mais próximo o chute, mais rápida vai ser nossa convergência!
Outro ponto fraco do método é a necessidade de resolvermos um sistema matricial a cada iteração. Se esse sistema tiver muitas equações será necessário muito poder computacional (ou manual no caso da prova haha) e o método acaba sendo muito custoso.
Quando é singular (tem o determinante igual a zero), o método de Newton pode não estar definido.
Método de Newton
Algoritmo
Observações
Exercícios Resolvidos
Exercício Resolvido #1
Lista da Professora Andretta – USP – Questão 6
Dado o sistema não linear
aplique uma iteração do Método de Newton para encontrar uma solução do sistema, a partir do ponto . Calcule os erros absoluto e relativo. O ponto calculado é uma boa aproximação para a solução do sistema?
Passo 1
Primeira coisa que temos que fazer é passar as constantes para o outro lado! Esse método é capaz apenas de encontrar o zero de funções não lineares! Assim, temos:
Onde,
A matriz Jacobiana fica:
Iteração 1:
Agora calculamos e com :
Resolvemos o sistema :
Chegando em:
Então,
Como podemos ver, o ponto calculado não é apenas uma boa aproximação, ele é uma solução do sistema! Logo, nossos erros absoluto e relativo serão iguais a zero.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 644, exercício 1.
Use o método de Newton com para calcular nos sistemas não-lineares abaixo:
Passo 1
Beleza, temos que:
Primeiro precisamos encontrar a matriz Jacobiana!
Iteração 1:
Agora calculamos e com :
Resolvemos o sistema :
Chegando em:
Então,
Normalmente agora seria a hora de testarmos o critério de parada, mas como a questão só pede para encontrarmos vamos continuar!
Iteração 2:
Calculando e :
Resolvemos o sistema :
Chegando em:
Então,
Passo 2
Agora temos:
Primeiro encontramos a matriz Jacobiana:
Iteração 1:
Agora calculamos e com :
Resolvemos o sistema :
Chegando em:
Então,
Iteração 2:
Calculando e :
Resolvemos o sistema :
Chegando em:
Então,
Passo 3
Nessa letra vamos ter que jogar as constantes pro outro lado, já que só sabemos achar o zero dessas funções! Então ficamos com:
Agora encontramos a matriz Jacobiana:
Iteração 1:
Agora calculamos e com :
Resolvemos o sistema :
Chegando em:
Então,
Iteração 2:
Calculando e :
Resolvemos o sistema :
Chegando em:
Então,
Passo 4
Temos:
A matriz Jacobiana será dada por:
Iteração 1:
Agora calculamos e com :
Opa, temos um problema aqui né? Não é possível obtermos pois demos de cara com um sistema de uma equação e duas variáveis! Quando uma linha da matriz Jacobiana zera, dizemos que ela é singular. Logo, não podemos continuar o exercício, pois é singular.
Resposta
Não podemos encontrar pois é singular.
Exercício Resolvido #3
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 644, exercício 2b e 2c.
Use o método de Newton com para calcular nos sistemas não-lineares abaixo:
Passo 1
Beleza, temos que:
Primeiro precisamos encontrar a matriz Jacobiana!
Iteração 1:
Agora calculamos e com :
Resolvemos o sistema :
Chegando em:
Então,
Normalmente agora seria a hora de testarmos o critério de parada, mas como a questão só pede para encontrarmos vamos continuar!
Iteração 2:
Calculando e :
Resolvemos o sistema :
Chegando em:
Então,
Passo 2
Nessa letra vamos ter que jogar as constantes pro outro lado, já que só sabemos achar o zero dessas funções! Então ficamos com:
Agora encontramos a matriz Jacobiana:
Iteração 1:
Agora calculamos e com :
Resolvemos o sistema :
Chegando em:
Então,
Iteração 2:
Calculando e :
Resolvemos o sistema :
Chegando em:
Então,
Resposta
Exercício Resolvido #4
Lista de Sistemas Não Lineares – UNICAMP – Questão 1
Se aplicarmos o método de Newton para sistemas não lineares para resolver um sistema linear , em quantas iterações o método irá convergir? Justifique sua resposta.
Passo 1
Eaí, alguma ideia? É, eu também não :p
Bom, só tem um jeito de descobrir então né! Vamos aplicar o método em um sistema linear e ver no que dá:
Isso nos deixa com um sistema do tipo:
Onde:
A matriz Jacobiana ia ficar:
E para qualquer aproximação que usarmos, teremos:
Assim, o sistema vai ficar:
Se multiplicarmos nos dois lados:
Lembrando que é a própria solução do sistema linear! Então:
Logo, teremos que:
Ou seja, sempre encontraremos a solução na primeira iteração!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Lista de Sistemas Não Lineares – UNICAMP – Questão 2
Considere o sistema não linear
que tem como solução .
Verifique que a matriz Jacobiana é invertível em
Resolva esse sistema através do método de Newton com
Passo 1
Calculando a matriz Jacobiana temos:
Em , temos:
Que não só é invertível, mas tem como inversa ela mesma, já que é a matriz identidade. Então está verificado haha.
Passo 2
Iteração 1:
Calculando e com :
Resolvemos o sistema :
Chegando em:
Então,
Que é um número estupidamente grande né? Isso aconteceu porque a matriz Jacobiana avaliada no ponto inicial era praticamente igual a matriz nula né? Eu diria que é bem próximo de zero haha.
E lembra que quando a matriz Jacobiana se iguala a zero temos uma matriz singular e não podemos continuar com o método? Então, foi exatamente isso que aconteceu aqui ;)
Resposta
Não podemos resolver o problema, pois é muito próximo da matriz nula.