Aproximação por Diferencial
Teoria
No ensino médio, sempre tinha uma questão que pedia velocidade média, onde:
Aqui, a gente viu que a velocidade instantânea é isso ai quando é muito pequeno ():
E que isso nada mais é que a derivada da posição ( e que pode ser representado pela notação de diferenciais:
Oxê, mas aonde você quer chegar com isso? Pela própria notação, percebemos que é para quando é muito pequeno e o mesmo vale para e . Então, quando e não são muito grandes:
Isso também é válido para qualquer variável: , e aquela letra grega que o professor coloca no quadro e ninguém nunca sabe qual é:
O importante é: dá para a gente usar essa ideia para aproximar alguns valores.
Imagine que um disco de ferro estava sobre o maravilhoso Sol do Rio de Janeiro e dilatou. Sua área variou. O quanto seu raio variou se o raio era de ?
Bem, é um disco. Então área será:
A primeira coisa que a gente tem que fazer, é derivar isso aí para chegar aos diferenciais:
Colocamos um diferencial em cada lado da equação:
E aproximamos os diferenciais pelos deltas:
Considerando a variação dá área e o raio :
É possível também que o problema não te dê nem a função, nem o valor da variação. Nesse caso, será pedida a aproximação de algum número irracional, como . Aí você deve escolher uma função que tenha um valor racional próximo, como:
Já que a função acima tem, para , um valor racional próximo do que a gente quer calcular .
E a variação será a diferença entre o ponto que a gente quer calcular () e o ponto que a gente sabe calcular, que foi para a função escolhida. Nesse caso:
Como a variação dependerá da função escolhida, você deve pensar nela depois de determinar a função. Lembre-se que o valor da variação deverá ser pequeno, então cuidado com suas escolhas!
Aí, com a função e o delta determinados, é só fazer o que a gente fez no primeiro exemplo. Agora, tente terminar a questão. Se você não conseguir, não tem problema. Tem um exercício igualzinho com placa de abraços grátis te esperando lá nos exercícios de fixação!
Para não escapar nada...
Como proceder com aquela letra grega que o professor coloca no quadro e ninguém nunca sabe qual é?
pode ser dita csi, é o epsilon, é o lamda, e são phi. é ômega, não w, é o mi e não u. Agora você já sabe cada uma delas ;-).
E se o problema tivesse dado o valor final e inicial da área, ao invés do valor da variação dela?
É só lembrar que a variação de ou qualquer outra variável é igual ao seu valor final menos o inicial. No caso da área:
Exercícios Resolvidos
Exercício Resolvido #1
Howard Anton, Irl Bivens, Stephen Davis, Cálculo – Volume I, 8ª ed. Porto Alegre: ARTMED EDITORA S.A, 2005, pg 230 exercício 37 b
Encontre a diferencial , onde
Passo 1
Para acharmos a diferencial , primeiro devemos derivar essa função em relação a :
Usamos a notação ao invés de , justamente para deixar a presença dos diferenciais.
Passo 2
Agora que temos a derivada, basta jogar o para o lado direito, assim a nossa diferencial vai ficar:
A grande complicação em simplesmente calcular o diferencial é na parte da derivada mesmo.
Resposta
Exercício Resolvido #2
Howard Anton, Irl Bivens, Stephen Davis, Cálculo – Volume I, 8ª ed. Porto Alegre: ARTMED EDITORA S.A, 2005, pg 231 exercício 50
Uma escada com está apoiada em uma parede e faz um ângulo com o chão. Se o topo da escada está a uma altura de na parede, expresse em termos de e, então, use para estimar a variação em se variar de a .
Passo 1
Bem, ele quer estimar a variação de , para isso, devemos relacionar e e calcular os diferenciais. A situação é que nem a da figura aqui embaixo:
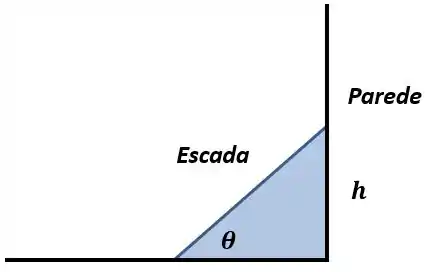
Como temos um triângulo retângulo, podemos fazer
Assim
Agora vamos achar a diferencial,
Agora passamos aquele para direita
Passo 2
Beleza, já sabemos o diferencial, o que falta agora é saber o ângulo e , lembrando que sempre que trabalhamos com ângulos eles precisam estar em radianos.
Repara que o começa em , então esse vai ser o nosso valor de , ele vai funcionar como o ponto de referência como vimos antes. Nessas situações de diferencial, vamos considerar sempre o inicial como o ponto central, beleza?
Agora falta achar , mas lembra da teoria? Nós fazemos a seguinte aproximação:
E esse ele deu no enunciado, que vai ser:
Agora temos que passar esses caras todos para radianos:
Passo 3
Agora vamos achar com tudo que já calculamos antes:
Então:
Assim, com a nossa aproximação, vamos ter:
Resposta
Exercício Resolvido #3
Elaboração Própria
Calcule o valor aproximado de usando diferenciais.
Passo 1
A primeira coisa a fazer é achar a função a derivar. A nossa função vai ser:
Pois está próximo e seu valor é conhecido. Agora vamos achar o diferencial.
Passando para o outro lado:
Passo 2
Falta acharmos o ponto de referência, ou inicial neste caso de diferencial. Vamos fazer que é perto do que ele pediu e sabemos fazer a raiz.
Agora que temos isso, vamos trocar o valor de que temos, para sabermos a diferencial ao redor de .
Achamos o diferencial ao redor do ponto. Agora que temos isso, vamos lembrar da teoria que:
E:
Assim, vamos começar achando isso porque sabemos o inicial e o final dessa variação:
Passo 3
Agora que temos vamos achar :
Vamos lembrar agora, da teoria, que podemos fazer a seguinte aproximação:
Assim, vamos ter:
Trocando os valores vamos ter:
Assim:
Resposta
Exercício Resolvido #4
Howard Anton, Irl Bivens, Stephen Davis, Cálculo – Volume I, 8ª ed. Porto Alegre: ARTMED EDITORA S.A, 2005, pg 231 exercício 57 – Modificado
Uma barra de metal medindo de comprimento e de diâmetro está coberta, exceto nas pontas, por uma camada de isolante com uma espessura de . Use Diferenciais para estimar o volume do isolante. Calcule também o volume do isolante de forma exata, e compare os resultados do valor real com a aproximação.
Passo 1
Bem, vamos começar entendendo o problema, temos uma barra de metal, que está revestida por um pequeno isolante.
Temos duas formas de fazer isso, podemos calcular na mão, que seria fazer o volume total com o isolante menos o volume total sem o isolante, e a outra forma seria fazer a aproximação, imaginando que esse volume do isolante nada mais é que a variação do volume quando o raio vai de para .
O problema pede os dois, mas calculando a aproximação que foi o que a questão pediu primeiro:
O volume desse cilindro vai ser
O é fixo, então podemos mudar logo o seu valor
Lembra da teoria que podemos relacionar com ? A diferencial do volume em relação ao raio vai ser
Passando o para direita,
Passo 2
Agora temos que:
Agora temos que achar o . Como vimos na teoria, vamos ter:
E:
Agora que temos , podemos achar , lembrando que o raio dessa fórmula, vai ser o raio inicial, como já vimos nos outros exercícios. Então:
E substituindo no valor da fórmula no fim do passo , temos:
Passo 3
Agora vamos fazer a conta real:
Assim:
Vamos ter:
Passo 4
Comparando a aproximação com o cálculo real:
Comparando os valores, podemos ver que eles são beeem próximos, o erro calculado nessa aproximação é bem pequeno.
Porém, como a gente quer as coisas o mais próximo possível do valor real, evitamos o cálculo por aproximação quando o cálculo real é possível. Afinal, você vai querer que aquele prédio que você assinou fique de pé.
Resposta
Exercício Resolvido #5
Uma esfera de madeira de de diâmetro é envernizada, ficando mais espessa. Use Diferenciais para estimar o volume da camada de verniz. Calcule também o volume do verniz de forma exata, e compare os resultados do valor real com a aproximação.
Passo 1
Bem, vamos começar entendendo o problema, temos uma esfera de madeira envernizada. Porque alguém enverniza uma esfera de madeira eu já não sei.
Temos duas formas de fazer isso, podemos calcular na mão, que seria fazer o volume total com o verniz menos o volume total sem o verniz, e a outra forma seria fazer a aproximação, imaginando que esse volume do verniz nada mais é que a variação do volume quando o raio vai de para (a questão dá o diâmetro)
O problema pede os dois, mas calculando a aproximação que foi o que a questão pediu primeiro:
O volume da esfera vai ser
Lembra da teoria que podemos relacionar com ? A diferencial do volume em relação ao raio vai ser
Passando o para direita,
Passo 2
Agora temos que:
Agora temos que achar o . Como vimos na teoria, vamos ter:
E:
Agora que temos , podemos achar , lembrando que o raio dessa fórmula, vai ser o raio inicial, como já vimos nos outros exercícios. Então:
E substituindo no valor da fórmula no fim do passo , temos:
Passo 3
Agora vamos fazer a conta real:
Assim:
Vamos ter:
Passo 4
Comparando a aproximação com o cálculo real:
Comparando os valores, podemos ver que eles são próximos, o erro calculado nessa aproximação é pequeno.
Porém, como a gente quer as coisas o mais próximo possível do valor real, evitamos o cálculo por aproximação quando o cálculo real é possível. Afinal, você vai querer que aquele prédio que você assinou fique de pé. Não é um prédio nesse caso mas a ideia é a mesma ;)