Teoria
Fala aí! Seja bem vindo ao Responde Aí! Bora aprender Valor Relativo em uma Diferencial?
O que é o Valor Relativo em uma Diferencial?
Antes de qualquer coisa, vamos dar um passinho pra trás!
Quando estudamos aproximação por diferencial vemos que quando consideramos um intervalo muito pequeninho em uma função, próximo de zero, podemos fazer a seguinte aproximação:
Esse raciocínio é muito usado quando a gente calcula a velocidade instantânea lá em Física.
Se tivermos um intervalo de tempo muito pequenininho, podemos aproximar a velocidade instantânea da velocidade média.
-Beleza, mas isso vai gerar um erro, não vai!?
SIM! É ai que entra o valor relativo! Imagina que você mede o tempo em que um velocista corre
Podemos então dizer que o valor médio será:
Com isso a gente pode calcular o erro relativo e o erro percentual!
Erro Relativo ou Percentual
O erro relativo nos dá a distância do valor obtido em relação ao valor exato, para isso usamos essa formulazinha aqui:
Agora, pra fechar com chave de ouro! Se liga nesse vídeo super completo sobre valor relativo!
Agora vamos praticar com exercícios?
Erro Relativo ou Percentual
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
O lado de um quadrado mede aproximadamente , com erro possível de .
- Use diferenciais para estimar o erro na área calculada.
- Estime o erro percentual no lado e na área.
Passo 1
a)
O erro da área nada mais é do que a variação da área, ou seja, . Além disso, vimos na teoria que:
Então só precisamos achar o diferencial dessa função da área. Vamos escrever a área em função do lado :
Assim, derivando:
Passando para direita:
Passo 2
Pela aproximação por diferencial, sabemos que:
Logo:
Agora que temos o diferencial da área, e que vimos que ela vai ser o erro, vamos calcular no intervalo que ele deu. Ele disse que o erro do lado vai entre e então:
Multiplicando por para dar o diferencial de ali no meio, temos:
Ele deu o ponto inicial do lado, que vai ser , então:
Esse vai ser o erro da área.
Passo 3
b)
Vamos achar agora os erros percentuais. O erro percentual nada mais é que o erro relativo que vimos na teoria.
Primeiro o erro do lado, para isso temos que dividir por . Já vimos que ele quer esse erro percentual com , e:
Assim:
E vamos ter:
Colocando em porcentagem e substituindo por
Passo 4
Vamos agora para o erro percentual da área, primeiro temos que achar a área para :
E o erro percentual da área vai ficar:
Colocando isso em porcentagem e substituindo por :
E achamos os erros percentuais.
Resposta
a)
b)
Exercício Resolvido #2
Elaboração Própria
A área de um triângulo retângulo com uma hipotenusa é calculada pela fórmula , onde é um dos ângulos agudos. Use diferenciais para aproximar o erro no cálculo de se (exatamente) e com erro possível de .
Além disso, determine o erro percentual no cálculo de .
Passo 1
Bem, aqui ele quer um aproximação do erro de e o erro percentual desse mesmo . Vamos começar achando o erro de , para isso vamos achar seu diferencial em relação a :
Podemos trocar o valor de nessa fórmula já que ele é constante:
O seu diferencial vai ser:
Passando para direita:
Passo 2
Agora que temos o diferencial, sabemos, pela teoria, que podemos relacionar com , e vai ser o erro na conta. Assim:
Além disso, também sabemos que pode ser aproximado por . Ele deu a variação de , então temos:
Esse é o intervalo do erro, vamos passar esses valores dos ângulos para radiano, porque sempre que trabalhamos com ângulo precisamos usar radianos:
Assim vamos ter:
Multiplicando isso por , vamos ter:
Assim, aquele cara do meio é :
Ele disse o valor de , que vai ser , vamos passar isso para radianos:
Assim, temos:
Ufa, achamos o intervalo do erro dessa área. Vamos recapitular o que fizemos. Achamos a fórmula da diferencial de , que vai ser o erro que ele está querendo. Depois nos achamos o intervalo que o erro de vai estar. Depois fizemos umas contas para chegar no intervalo de , que é só ir multiplicando a função no valor de que for o ponto inicial, ou ponto central.
E pronto temos o nosso intervalo.
Passo 3
Vamos agora achar o erro percentual dessa parada, para isso temos que achar o erro relativo, que é a mesma coisa
Então precisamos achar o valor de no valor inicial de
Já sabemos o intervalo de , então basta dividir geral nesse intervalo por , que achamos o erro relativo
Fazendo essa conta na calculadora vamos ter:
Passando para porcentagem e substituindo por vamos ter o erro percentual variando entre:
Resposta
Exercício Resolvido #3
Elaboração Própria
Uma piscina no formato de um trapézio isósceles tem sua área dada pela fórmula . Abaixo, uma representação dessa piscina:
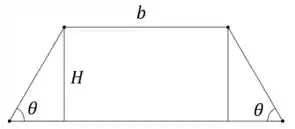
Use diferenciais para aproximar o erro no cálculo de se (exatamente), (exatamente) e com erro possível de .
Além disso, determine o erro percentual no cálculo de .
Passo 1
Bem, aqui ele quer um aproximação do erro de e o erro percentual desse mesmo . Vamos começar achando o erro de , para isso vamos achar seu diferencial em relação a :
Podemos trocar o valor de e de nessa fórmula já que ele é constante:
O seu diferencial vai ser:
Por fim:
Passando para direita:
Passo 2
Agora que temos o diferencial, sabemos, pela teoria, que podemos relacionar com , e vai ser o erro na conta. Assim:
Além disso, também sabemos que pode ser aproximado por . Ele deu a variação de , então temos:
Esse é o intervalo do erro, vamos passar esses valores dos ângulos para radiano, porque sempre que trabalhamos com ângulo precisamos usar radianos:
Assim vamos ter:
Multiplicando isso por , vamos ter:
Assim, aquele cara do meio é :
Ele disse o valor de , que vai ser , vamos passar isso para radianos:
Assim, temos:
Ufa, achamos o intervalo do erro dessa área. Vamos recapitular o que fizemos. Achamos a fórmula da diferencial de , que vai ser o erro que ele está querendo. Depois nos achamos o intervalo que o erro de vai estar. Depois fizemos umas contas para chegar no intervalo de , que é só ir multiplicando a função no valor de que for o ponto inicial, ou ponto central.
E pronto temos o nosso intervalo.
Passo 3
Vamos agora achar o erro percentual dessa parada, para isso temos que achar o erro relativo, que é a mesma coisa
Então precisamos achar o valor de no valor inicial de
Já sabemos o intervalo de , então basta dividir geral nesse intervalo por , que achamos o erro relativo
Fazendo essa conta na calculadora vamos ter:
Passando para porcentagem e substituindo por vamos ter o erro percentual variando entre:
Resposta
Exercício Resolvido #4
Elaboração Própria
Uma menina muito curiosa resolveu calcular a área superficial e o volume de uma corda bem grossa. Sabendo que a corda tinha comprimento suficiente, e exato, para envolver um bambolê de de raio e que a corda tinha raio exato de . O erro possível de cálculo do raio da corda é de Estime:
- O erro e o erro percentual do cálculo da área superficial da corda
- O erro e o erro percentual do cálculo do volume da corda
OBS: A menina sabe que, independente de calcular como ela fez esse cálculo, a proporção entre o raio do bambolê e da corda é fixa.
Passo 1
Quando a gente vê um OBS numa questão, geralmente é pra gente ficar atento porque tem dica boa aí! Nesse caso, como a menina sabe a proporção, a gente precisa saber também!
Ela não sabe as medidas exatas dos raios, nós sabemos. Se o raio do bambolê é e o raio da corda é , então:
Ta, mas e daí? Bem, a gente vai poder usar essa proporção pra escrever o volume e a área superficial da corda em função de uma variável só. Quer ver? Se a corda é um cilindro, temos que sua altura vale:
Que nada mais é do que o comprimento do bambolê. E a área da base desse cilindro vai ser então:
Show de bola, calculamos então o volume e a área superficial por:
O que fica:
Passo 2
Agora vamos calcular o diferencial das funções de que vimos acima. Saca só:
E passando por outro lado o :
Agora que temos o diferencial, sabemos, pela teoria, que podemos relacionar com e relacionar com . e vão ser o erro na conta. Assim:
Além disso, também sabemos que pode ser aproximado por . Ele deu a variação de , então temos:
Esse é o intervalo do erro. Multiplicando isso por , vamos ter:
Assim, aquele cara do meio é :
Pro volume, basta então a gente multiplicar o intervalo de variação do erro do raio por :
Sendo que o valor de ali dentro é o valor inicial, dado no enunciado, de , logo:
Passo 3
Vamos agora achar o erro percentual dessas paradas. Para isso temos que achar o erro relativo, que é a mesma coisa
Então precisamos achar o valor de no valor inicial de :
E o valor de no valor inicial de também:
Já sabemos o intervalo de , então basta dividir geral nesse intervalo por , que achamos o erro relativo:
Passando para porcentagem e substituindo por vamos ter o erro percentual variando entre:
Agora, pro cálculo do volume, fazemos a mesma coisa, beleza? Já sabemos o intervalo de , então basta dividir geral nesse intervalo por , que achamos o erro relativo:
Passando para porcentagem e substituindo por vamos ter o erro percentual variando entre:
Resposta
Exercício Resolvido #5
Elaboração Própria
Um professor um pouco pirado entregou pra seus alunos o gráfico da curva e pediu para que calculassem a área abaixo do gráfico entre e . Os alunos optaram por calcular essa área usando um triângulo retângulo cuja hipotenusa tangenciasse a curva. Abaixo, uma representação de como esse triângulo muda em função do ponto de tangência:
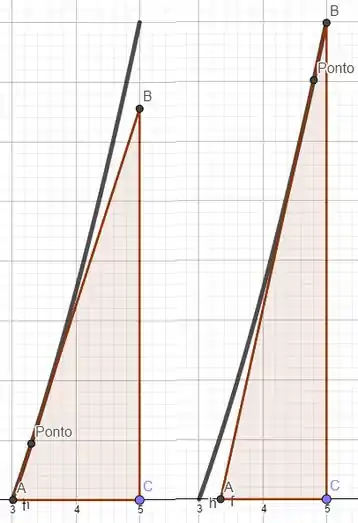
Sabendo que os alunos escolheram como ponto de tangência e que o erro na marcação desse ponto é de calcule o erro percentual no cálculo de . Depois, calcule também o mesmo erro em relação à área real abaixo da curva.
Passo 1
Bem, aqui ele quer um aproximação do erro de e o erro percentual desse mesmo . A nossa dificuldade nessa questão vai ser achar a expressão de em função de uma variável pra podermos variar. De qualquer forma, a área do retângulo vai ser:
Mas quem vai ser a base e a altura? Pô, o truque pra tirar de letra quem vai ser e é lembrar que a hipotenusa desse triângulo é uma reta tangente, e retas tangentes tem a seguinte expressão:
Onde é o ponto de tangência na curva . Escolhendo um ponto de tangência qualquer , vamos ficar com:
Esse nada mais é do que a inclinação da reta tangente no ponto de tangência, lembra? Então a gente calcula ele tranquilin assim ó:
E a equação da reta tangente é reescrita para:
Como a altura desse triângulo está sempre, pela figura, em cima de , temos que:
Show, falta achar a base agora. Se a gente olhar pro esquema do enunciado vemos direitinho que a base vai ser sempre “menos algo”. E olha só! Não é que esse “algo” vai ser sempre o valor de em que a reta tangente toca o eixo ? Sendo assim, a base vai ser:
A base vai ser então:
E a área vai ser:
Passo 2
Nesse passo, vamos fazer o diferencial, beleza? Já que , o diferencial vai ficar:
Passando pro outro lado:
Agora que temos o diferencial, sabemos, pela teoria, que podemos relacionar com , e vai ser o erro na conta. Assim:
Além disso, também sabemos que pode ser aproximado por . Ele deu a variação de , então temos:
Multiplicando isso por , vamos ter:
Assim, aquele cara do meio é :
Ele disse o valor de , que vai ser , segundo o enunciado, a gente substitui:
Assim, temos:
Passo 3
Vamos agora achar o erro percentual dessa parada, para isso temos que achar o erro relativo, que é a mesma coisa
Então precisamos achar o valor de no valor inicial de , que é
Já sabemos o intervalo de , então basta dividir geral nesse intervalo por , que achamos o erro relativo
Passando para porcentagem e substituindo por vamos ter o erro percentual variando entre:
Graficamente da pra ver que a área desse triângulo não é muito diferente da área abaixo da curva, saca só:
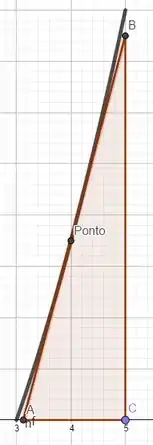
Se usássemos como no calculo do erro relativo a área real, teríamos que fazer:
O erro relativo seria:
E por fim:
Resposta
Em relação à área calculada pelos alunos:
Em relação à área real: