Aproximação Linear
Produzido por Arthur Melo de AlmeidaTeoria
Fala aí, você acaba de chegar no Responde Aí! E aqui vamos te explicar tudo sobre aproximação linear
Aproximação linear
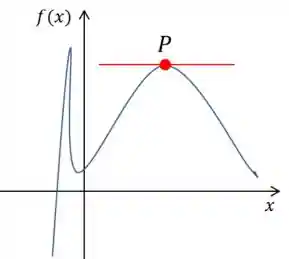
Olha essa curva de função aqui. Agora eu quero achar a reta que descreve essa região próxima ao ponto
Porém tem um detalhe a reta tangente é sempre a melhor reta!
Ou seja, toda vez que te perguntarem por aproximação linear, você já sabe que tem que aproximar algo usando reta tangente!
A reta tangente tem a equação geral:
E se o seu professor perguntar por uma definição formal de aproximação linear, você pode dizer assim:

Exemplo
Calcule a aproximação linear da função
Passo 1: Pra começar, vamos descobrir o valor de
Passo 2: Agora vamos calcular a derivada de
E calculamos o valor de
Passo 3: Agora é só aplicar na fórmula da reta tangente:
Logo:
Videoaula
Pra ficar ligado e não perder nada do conteúdo, que tal conferir uma videoaula?
E pra completar, dá uma olhada em uns exercícios 👇
Exemplo
Videoaula
Exercícios Resolvidos
Exercício Resolvido #1
Howard Anton, Irl Bivens, Stephen Davis, Cálculo – Volume I, 8ª ed. Porto Alegre: ARTMED EDITORA S.A, 2005, pg 230 exercício 4 a
Encontre a aproximação linear local da função em e use-a para aproximar e .
Passo 1
Aqui ele quer a aproximação linear daquela função em torno daquele valor de que ele deu.
Então a primeira parte, que é achar essa aproximação é bem de boa, lembra da fórmula da aproximação linear? Ela vai ser:
A primeira coisa a fazer é achar a derivada de :
Passo 2
Agora que temos a derivada, vamos jogar na fórmula da nossa aproximação linear, lembrando que , a nossa aproximação linear vai ficar:
E essa é nossa aproximação linear. =D
Passo 3
Vamos agora estimar os valores que ele quer usando essa aproximação linear.
Começando com , a nossa função é , assim para esse valor que ele pediu vamos ter
Então vamos ter:
Passo 4
Vamos agora para o outro valor que ele pediu, , a nossa função é , assim para esse valor que ele pediu vamos ter
Então vamos ter
Resposta
Exercício Resolvido #2
UNICAMP - Cálculo 1 - P2 2015 Noturno Sexta – 1
Considere a curva definida pela equação . Calcule e encontre a aproximação linear à curva no ponto .
Passo 1
Temos ali uma função implícita. Para fazer a aproximação linear (que é a reta tangente à curva) no ponto precisamos do valor de , para o qual precisamos da fórmula implícita de . Para isso, vamos derivar implicitamente o termo pelas Regras do Produto e da Cadeia:
Eis o nosso em função de e de .
Passo 2
A aproximação linear terá o formato:
O ponto é o valor fornecido na questão:
E será o valor da implícita nesse ponto:
Agora é substituir os valores:
Que será nossa aproximação linear!
Resposta
Exercício Resolvido #3
Howard Anton, Irl Bivens, Stephen Davis, Cálculo – Volume I, 8ª ed. Porto Alegre: ARTMED EDITORA S.A, 2005,Pg 230 exercício 28
A aproximação é frequentemente usada por engenheiros para cálculos rápidos.
Deduza esse resultado e use-o para fazer uma estimativa grosseira de
Passo 1
Aqui ele quer que verifiquemos aquela aproximação que ele deu. Ele está aproximando a equação por uma reta, então isso é uma aproximação linear.
A grande questão aqui é qual a função que ele usou para aproximar e qual o ponto de referência.
A função é mais de boa de achar, isso porque ele aproxima , e essa vai ser nossa função:
Passo 2
Agora temos que achar o ponto de referência, para isso vamos fazer a aproximação linear para um ponto de referência qualquer , primeiro precisamos da derivada de
A aproximação linear vai ser:
Trocando os valores de e vamos ter:
Arrumando isso:
Vamos comparar isso com a equação que ele deu ali em cima:
Isso nos diz que:
E:
Pela primeira equação vamos ter:
Vamos substituir isso na segunda expressão:
Assim, como pode ser qualquer valor:
E temos o nosso ponto de referência, e a aproximação linear foi como ele queria.
Passo 3
Vamos agora fazer a aproximação do valor que ele pediu, . Vamos ter, neste caso, . Além disso devemos achar qual valor de vamos usar na função, então vamos fazer
Assim:
A nossa aproximação linear vai ficar:
Resposta
Exercício Resolvido #4
Elaboração Própria
A aproximação linear da função , no ponto de referência , é:
Determine o ponto de referência.
Passo 1
Opa, temos um exercício um pouco diferente aqui. Ele nos deu a aproximação linear e quer o ponto de referência. Vamos fazer a aproximação linear para um ponto qualquer e vamos comparar com essa aproximação que ele deu.
Passo 2
Para fazermos a aproximação linear precisamos da função , da sua derivada e do ponto de referência .
Primeiro vamos achar a derivada dessa parada
Assim nossa aproximação linear vai ser:
Trocando os valores de e temos:
Arrumando isso temos:
Passo 3
Vamos agora comparar isso que achamos com o que ele deu:
Para isso ser sempre igual devemos ter:
A segunda equação é impossível de resolver na mão, então vamos nos preocupar em resolver a primeira, e depois só verificar com a segunda.
Temos:
Lembra da relação entre secante e tangente?
Assim vamos ter, na nossa equação:
Colocando em evidência, vamos ter:
Assim vamos ter duas equações:
E:
Onde e são inteiros.
Resolvendo essas equações logarítmicas:
Passo 4
Achamos os possíveis valores de pela primeira equação, a parada agora é substituir esses valores na segunda equação e ver quais deles que servem para nós.
Substituindo o primeiro valor de , :
Nessa situação a secante de algum múltiplo inteiro de pode ser ou , mas como a secante está ao quadrado:
Assim temos:
E achamos um dos possíveis pontos de referência:
Passo 5
Para outra solução de , qual o valor de que serve nessa parada?
Substituindo o segundo valor de , , vamos ter:
Passo 6
Observa que
Além disso,
Portanto,
Só pode assumir dois valores ou . Como no nosso exercício ela está elevada ao quadrado, não faz diferença, vamos ter que
Passo 7
Assim, temos que
Queremos os valores de , então vou aplicar dos dois lados, vem comigo
Portanto, nosso outro ponto de referência será
Resposta
Exercício Resolvido #5
Elaboração Própria
Determine o valor de usando aproximação linear em uma função da sua escolha em torno do ponto .
Com esse valor aproximado de determine o valor de .
Passo 1
Bem, aqui ele quer que calcule aquele valor:
Mas ele não diz qual a função que vamos usar, só diz o ponto que temos que usar. Neste caso podemos usar qualquer função que acharmos melhor. Vamos sempre tentar olhar a mais fácil possível.
Repara que ele quer elevado a algo, assim isso nos dá a dica de usarmos:
Até porque essa função no ponto de referência que ele deu é tranquila de calcular. Vamos ver se a derivada também é de boa:
Opa, também é tranquilo de calcular. Então vamos usar essa função mesmo.
Passo 2
Agora que escolhemos a função, agora vamos fazer a aproximação linear
Trocando o valor de , e vamos ter:
Passo 3
Agora que temos a nossa aproximação linear, vamos achar o valor que ele pediu. A primeira coisa é ver qual o valor de , nesse caso mesmo.
Nessas questões que nós vamos escolher a função, vamos tentar evitar coisas muito loucas e usar o mais simples para não se embolar depois.
Temos:
Passo 4
Agora que temos esse valor de , para acharmos basta elevar esse número a , então: