18. Use o método de Newton para encontrar todas as raízes da equação com precisão de seis casas decimais.
Passo 1
Fala aí, eu sou o Rafha do Responde Aí e vou te ajudar em mais uma questão!
Aqui temos a seguinte equação:
E queremos encontrar a sua raiz, isso é, o valor de para o qual:
De forma que nossa função a qual queremos encontrar a raíz é portanto:
E queremos encontrar todas as suas raízes.
Para isso vamos usar um método iterativo que é o método de Newton.
Basicamente, nós começamos com um chute inicial para essa raiz.
E para encontrar o próximo valor, faremos a seguinte iteração:
O enunciado pede para encontrarmos com uma precisão de seis casas decimais, dessa forma, teremos que ir realizando iterações até que o valor encontrado não se altere até a sexta casa decimal.Dá trabalho? Dá... mas a vida é um morango mesmo!
Passo 2
No nosso método iterativo, temos que:
Dessa forma, precisamos da derivada de
Antes de derivar, vamos reescrever essa função em forma de potência:
Usando a regra da potência e também a regra da cadeia, teremos:
Logo,
Passo 3
Pronto, agora que é só jogar na fórmula de Newton:
Vamos agora analisar qual valor usar para .
Para isso, podemos usar a seguinte estratégia. Queremos que:
Isso é o mesmo que:
O gráfico de é igual ao gráfico de transladado em unidade para a esquerda. Já o gráfico de é igual ao gráfico de subtraído o gráfico de , esse não é tão simples de esboçar, mas com algum esforço você consegue, se liga só:
Fazendo e temos:
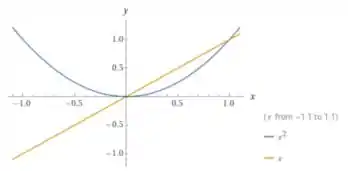
Agora uma menos o outro, ou seja, , podemos ir vendo o que ocorre ponto a ponto. Por exemplo, em , o resultado é algo positivo próximo de . Em , o resultado é . Em , o resultado também é . Provavelmente a parábola menos a reta, resulta em uma parábola. De fato, plotando , temos:
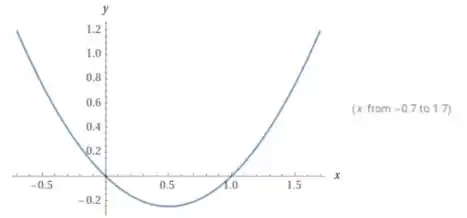
Agora que chegamos nesse gráfico, vamos esboça-lo junto com o :
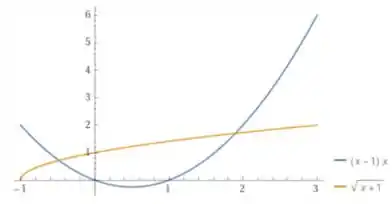
Olhando o gráfico, vemos que eles se interceptam próximo de e .
Vamos usar esses valores para chutes iniciais e encontrar quais são as verdadeiras raízes.
Passo 4
Para a primeira raiz vamos usar :
Fazendo as contas:
Para achar o processo é análogo. Logo,
Para :
Para :
Opa, como deu igual já podemos parar.
Passo 5
Para a segunda raiz vamos usar :
Fazendo as contas:
Para acharmos próximos o processo é o mesmo. Logo,
Para :
Para :
, então podemos parar.
Portanto, as raízes com aproximação de seis casas decimais são e
Resposta
As raízes com aproximação de seis casas decimais são e