Choque de Partículas e Interseção de Curvas
Produzido por Mariana PessanhaTeoria
Como saber?
Imagine que duas partículas descrevam trajetórias diferentes parametrizadas por duas funções diferentes:
E
Duas perguntas:
- As trajetórias dessas partículas se cruzam?
- Essas partículas se chocam?
Respondendo às perguntas:
- As trajetórias se cruzarão se houver pelo menos um ponto em comum nas duas curvas, não necessariamente no mesmo tempo ;
- As partículas se chocarão se houver um ponto em comum nas duas trajetórias, necessariamente no mesmo tempo .
Da primeira equação temos
Substituindo na segunda
E, como
Portanto, no instante para a primeira trajetória e no instante correspondente para a segunda trajetória, as partículas se cruzam. Para obter os pontos de cruzamento, basta calcular OU , porque eles correspondem ao mesmo ponto, concorda?
Escolhendo o ponto onde as trajetórias se cruzam é:
Esse corresponde ao sistema anterior, com .
Já resolvemos esse sistema e vimos que , então as partículas colidem.
Faz sentido? No primeiro caso, pode ser que uma partícula passe por um ponto em que a outra já passou antes ou ainda vai passar depois. No segundo caso, as partículas passam pelo mesmo ponto, ao mesmo tempo e por isso colidem.
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Duas partículas descrevem as curvas e especificadas abaixo. Determine se as trajetórias dessas partículas se cruzam em algum ponto. Verifique também se as partículas colidem ou não.
Passo 1
Fazer a igualdade e encontrar sistema:
Logo:
Passo 2
Resolver o sistema:
Verifique se a solução do sistema é essa:
Passo 3
Calcular ou para encontrar o(s) ponto(s):
Vamos calcular por exemplo:
Passo 4
Verificar se há colisão:
Acabamos de ver que há um único ponto em que as trajetórias se encontram. E vimos que .
Logo, as partículas não colidem!
Resposta
As trajetórias se encontram no ponto e as partículas não colidem, pois
Exercício Resolvido #2
UFRJ, Cálculo Diferencial e Integral 2, P1 2010.2, questão 3.4
Uma partícula se move ao longo da curva definida por
E uma partícula se move ao longo da curva definida por
Em que pontos as trajetórias dos pontos e se cruzam? As partículas vão colidir?
Passo 1
Vamos resolver o item (a):
Fazer a igualdade e encontrar sistema:
Logo:
Passo 2
Resolver o sistema:
Vamos reescrever a segunda equação evitando o termo com o cosseno ao quadrado. Lembre-se de que podemos sempre dizer que:
Remanejando esse resultado, temos então que:
Logo:
Vamos reescrever nossas equações:
Passo 3
Observe que a tanto na primeira quanto na segunda equação, os termos devem ser positivos. Na primeira, porque temos um número elevado ao quadrado de um lado da equação. E na segunda porque temos uma raiz quadrada.
Então podemos elevar a primeira equação por e a segunda por :
Passo 4
Igualando os segundos membros das equações, encontramos o seguinte:
Chamemos :
Então:
Passo 5
Lembrando que o enunciado nos diz que , podemos então encontrar as soluções dessas equações:
Observe que não há nenhum valor para cujo é negativo. Por isso, a última equação não tem solução.
Passo 6
Agora vamos calcular os respectivos valores de para cada valor de :
Observação: Da equação , sabemos que , por isso na segunda equação acima!
Passo 7
Calcular ou para encontrar o(s) ponto(s):
Parece mais convidativo calcular :
Passo 8
Maravilha! E as partículas colidem?
Claro que não! Pois nos dois casos.
Logo, as partículas nunca colidirão!
Resposta
As trajetórias se cruzam em e .
As partículas não vão colidir.
Exercício Resolvido #3
UFRJ, Cálculo Diferencial e Integral 2, PF 2015.1, questão múltipla escolha 8
Uma partícula tem seu movimento no plano descrito pela parametrização Então podemos afirmar que:
(a) a partícula passa pela reta
(b) nenhuma das outras alternativas.
(c) a partícula passa pela reta
(d) a partícula passa pela reta
(e) a partícula passa pela reta
Passo 1
A função é decrescente então
E como a exponencial é sempre positiva:
E também temos pras funções trigonométricas
Logo:
A partícula segue a parametrização ), então ela vai estar restrita a uma determinada área do plano, com
e
Que nada mais é que esse quadrado aqui
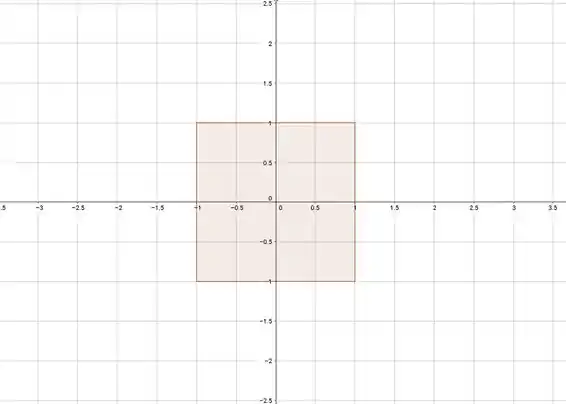
Passo 2
Show! Então vamos ver se alguma das retas que ele deu cruzam nosso quadrado! São as retas
São retas bem parecidas, na forma
Repare que por causa desse , nunca vamos ter ao mesmo tempo . Então as retas não cruzam o quadrado!
Vou acrescentá-las na nossa figura pra te convencer (na hora da prova você pode fazer uma também no canto da folha que é a boa):
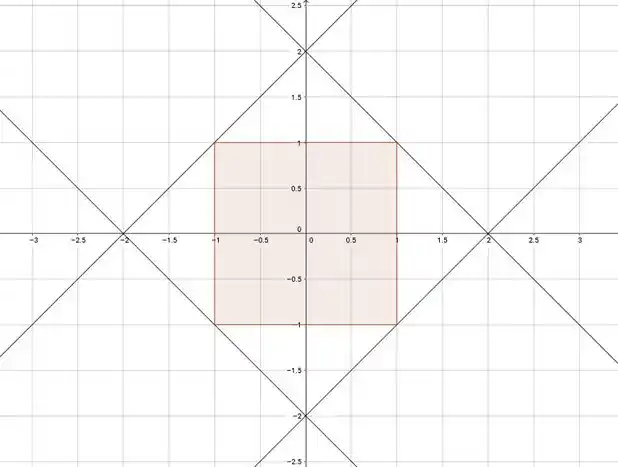
As retas passam raspando mas não cruzam o quadrado! E se fosse considerar essa raspada teríamos 4 alternativas certas né, então a resposta é a letra (b)!
Resposta
Alternativa (b)
Exercício Resolvido #4
UFRJ, Cálculo Diferencial e Integral 2, PF 2014.1, questão múltipla escolha 7
Duas partículas se movem no espaço e suas posições são dadas por
para . Suas trajetórias descrevem curvas e , respectivamente.
(a) As partículas não se chocam, porém as curvas e se interceptam nos pontos e .
(b) As curvas e não se interceptam.
(c) As partículas não se chocam, porém as curvas e se interceptam nos pontos e .
(d) As partículas se chocam nos pontos e .
(e) As partículas se chocam somente no ponto .
Passo 1
Vamos primeiro testar se as partículas se chocam, ok? O choque significa ocupar a mesma posição no espaço no mesmo tempo , ou seja
Isso nos dá um sistema:
A primeira equação dá:
Podemos ver facilmente que as outras equações não vão dar certo! A gente teria que ter
o que é totalmente errado!
Logo, as partículas não se chocam. Já eliminamos as 2 últimas alternativas! :)
Passo 2
Agora, se as curvas se interceptam, isso significa que as partículas ocuparam a mesma posição no espaço em tempos diferentes e . Então temos
Caímos no sistema
Pelas equações e , temos
Se :
Se :
Passo 3
Obtivemos os tempos em que e se interceptam: : e .
Portanto, as curvas se interceptam em 2 pontos:
e
Beleza... chegamos na alternativa (a) como resposta, maaaaass...
Passo 4
E se a gente tivesse escolhido as equações e , no passo 2 a gente ficaria com:
Daí temos ou:
Que já analisamos lá em cima e vai dar o ponto (1,1,1), né?
Ou temos:
Que dá, ou:
Que também já analisamos.
Maaaasss vai aparecer um valor novo pra
Hmmm... isso poderia virar outro ponto, né?
Mas só se fosse número normal e tals, mas estamos falando de tempo e não existe tempo negativo. AHAAAA
Então ta tudo certo mesmo e a respota certa é a alternativa (a)
=)
Resposta
Alternativa (a)