Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Vetor Tangente e Vetor Velocidade

Ver Todos os Exercícios

Teoria

Opaaa! Bora conversar um pouquinho sobre vetor tangente, vetor velocidade e de quebra ainda aprender como derivar funções vetoriais?! 🤩

Vetor Tangente

O vetor tangente é o vetor que toca a curva em um determinado ponto e tem a mesma direção do movimento!

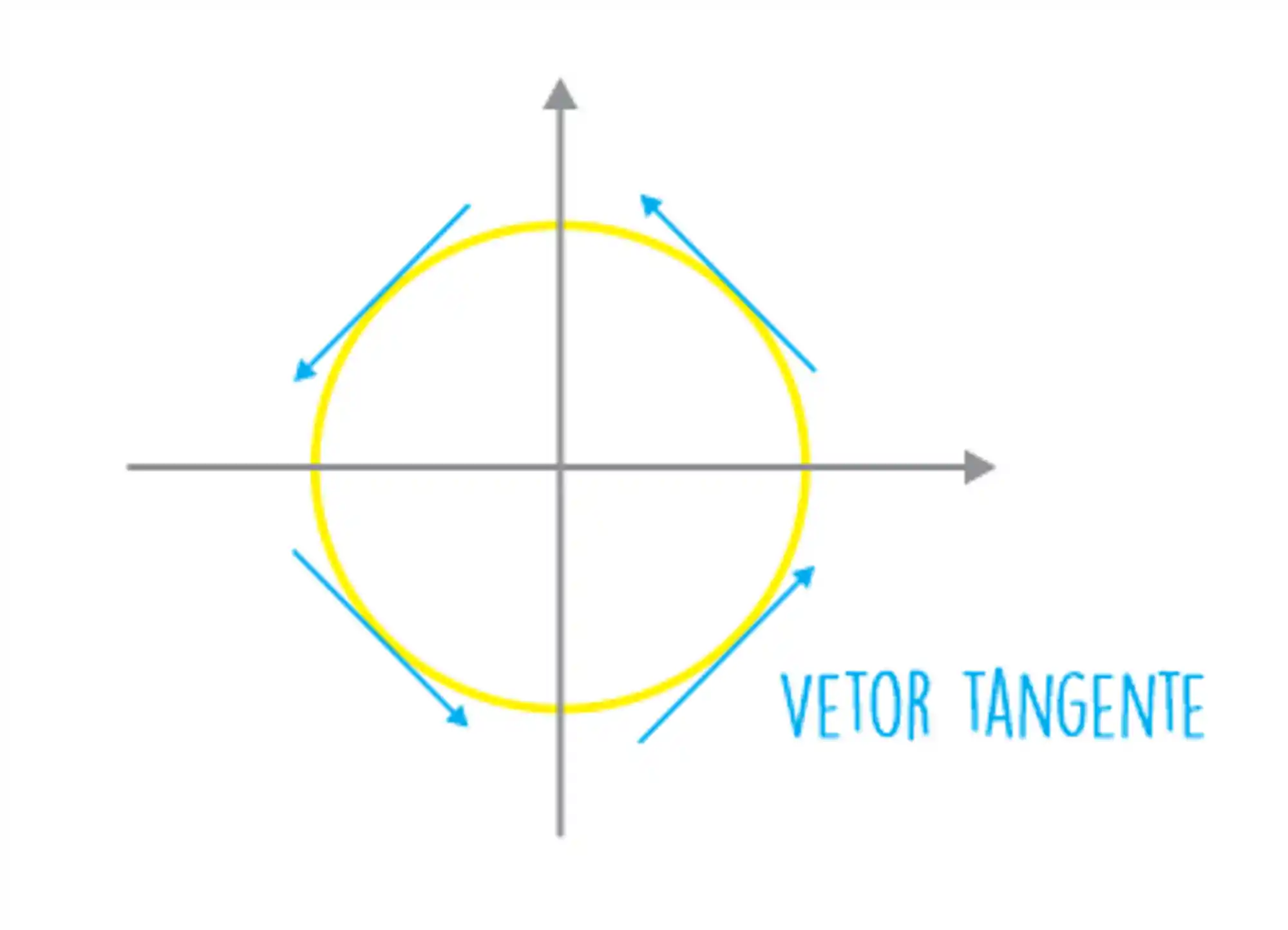
Vetor tangente
Vetor tangente

Ele é encontrado derivando o vetor posição.

Por exemplo:

²

-Mas como eu faço pra derivar um vetor?! 😖😖

📢 Clique para ver mais:

Não precisa se preocupar! É muuuuito mais simples do que parece. Se liga 👇👇👇

Derivada de uma Função Vetorial

Pra a gente derivar uma função vetorial, tudo o que precisamos fazer é derivar cada elemento individualmente:

²

Prontinho, é só isso mesmo! Se quisermos a segunda derivada por exemplo:

E assim por diante…sem nenhum mistério! Quer ver mais exemplo? Então se liga nesse vídeozinho super completo que o Responde Aí preparou pra você 👇👇👇

Vetor Velocidade

O vetor velocidade considera a variação da posição da partícula em relação ao tempo. Vamos considerar a trajetória de uma partícula dada pela curva , que é parametrizada por:

Que é uma função que fornece a posição da partícula em qualquer instante de tempo t, quando derivamos esse vetor posição o que você acha que encontramos? O vetor velocidade da partícula. Logo:

No nosso exemplo:

Se quisermos saber a velocidade escalar da partícula, isto é, a magnitude da velocidade, o que temos que fazer é calcular o módulo do vetor velocidade. Assim:

²
²²²

Quando estamos falando de vetor velocidade, o parâmetro  representa sempre o tempo. Logo, esse vetor tem a mesma direção do movimento da partícula. Em alguns casos, o vetor posição pode estar parametrizado em função de um ângulo, como é o caso da circunferência ou da elipse, por exemplo, a gente tem que colocar o parâmetro ângulo  em função do tempo .

Para fazer isso, é preciso relembrar alguns conceitos:

  • Movimento Circular Uniforme: é quando um corpo se move em uma trajetória circular, com velocidade constante. Nesse caso:

  • Movimento Circular Uniformemente Variado: é quando um corpo se move em uma trajetória circular, mas tendo sua velocidade variando com uma taxa constante, isto é, com aceleração constante. Nesse caso:

    ²

    Sendo a posição angular do corpo, a posição angular inicial, a velocidade angular do corpo, a velocidade angular inicial e a aceleração angular!

    Agora vamos praticar com exercícios?

Vetor Velocidade

Exercícios Resolvidos

Exercício Resolvido #1

George B. Thomas, Cálculo Volume II,11 ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pg. 238, exercício 1.

r t = t + 1 i + t 2 - 1 j é a posição de uma partícula no plano x y no instante t . Encontre o vetor velocidade da partícula no instante t = 1 .

Passo 1

Temos:

x t = t + 1

y t = t 2 - 1

Para achar o vetor velocidade temos apenas que derivar cada coordenada do vetor posição

Passo 2

Assim:

x ' t = 1

y ' t = 2 t

Substituindo em t = 1 :

x ' t = 1

y ' ( t ) = 2 1 = 2

Logo, a velocidade da partícula é v t = 1 i + 2 j

Resposta

A velocidade da partícula é v t = 1 i + 2 j

Exercício Resolvido #2

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p.22. questão 7.

Dois carros R 1 e R 2 percorrem, respectivamente, as estradas BR-101 e BR-102, tendo os seus movimentos descritos por

σ 1 t = 10 t , 50 t 2 e σ 2 t = ( 7 t ,   70 t - 50 ) , t ≥ 0

  1. No ponto P onde as estradas BR-101 e BR-102 se cruzam está situado um posto de fiscalização de velocidades. Encontre esse ponto P .
  2. Sabendo que o limite de velocidade em qualquer estrada brasileira é de 80   km / h , qual dos dois será multado no ponto P ?

Passo 1

Vamos resolver o item (a):

Se as rodoviais se cruzam nesse ponto P , devemos igualar as expressões σ 1 e σ 2 para encontra-lo.

Fazer a igualdade e encontrar sistema:

σ 1 t 1 = σ 2 ( t 2 )

10 t 1 ,   50 t 1 2 = ( 7 t 2 ,   70 t 2 - 50 )

Logo:

10 t 1 = 7 t 2 50 t 1 2 = 70 t 2 - 50

Passo 2

Resolver o sistema:

Na primeira equação podemos isolar t 2 :

t 2 = 10 7 t 1

E substituindo na segunda equação encontramos que

50 t 1 2 = 70 10 7 t 1 - 50

⇒ t 1 2 - 2 t 1 + 1 = 0

Essa equação do segundo grau admite uma única raiz:

t 1 = 1

Logo:

t 2 = 10 7

Passo 3

Para encontrar o ponto, basta calcular σ 1 ( t 1 ) ou σ 2 ( t 2 ) .

Logo:

σ 1 t 1 = ( 10 ,   50 )

Então:

P = ( 10 ,   50 )

Passo 4

Agora, precisamos saber as velocidades escalares dos dois carros quando passam pelo ponto P para descobrir qual deles ultrapassa 80   km / h .

Calculando velocidades vetoriais:

v 1 t = σ 1 ' t = ( 10 ,   100 t )

v 2 t = σ 2 ' t = ( 7 ,   70 )

Calculando velocidades escalares:

V 1 t = v 1 ( t ) = 10 2 + 100 t 2

V 2 t = v 2 ( t ) = 7 2 + 70 2

Calculando velocidades escalares no ponto P :

V 1 t 1 = 10 2 + 100 t 1 2 = 10 2 + 100 2 ≈ 100,5

V 2 t 2 = 7 2 + 70 2 ≈ 70,3

Logo, é o carro R 1 que será multado no ponto P .

Resposta

  1. P = ( 10 ,   50 )

O carro R 1 será multado no ponto P

Exercício Resolvido #3

Curvas Parametrizadas, Função Vetorial e Matriz Jacobiana

Uma partícula se move de acordo com a lei de movimento r t = 2 t , t 2 - 1 , t 2 + 1 , para t ∈ R .

a) Determinem, caso existam, as posições e velocidades da partícula nos instantes em que ela atinge os plano x O z , x O y e y O z .

Passo 1

Vamos lá, para descobrir as velocidades das partículas precisamos derivar a equação da trajetória, certo? Fazendo isso, teremos:

r ' t = 2,2 t , 2 t

Pronto, só isso mesmo :D

Passo 2

Agora que temos a equação que define a velocidade, temos que nos perguntar: qual é o valor de t para quando a partícula passa pelos planos x O z , x O y e y O z ?

Bom, para ela passar pelo plano x O z , então, para a equação da posição, devemos ter coordenada y = 0 , certo?

Dessa forma, temos:

t 2 - 1 = 0

t = ± 1

Quando t = 1 , a posição e velocidade dela valem:

r 1 = 2,0 , 2

r ' 1 = 2,2 , 2

Quando t = - 1 , a posição e velocidade valem:

r - 1 = - 2,0 , 2

r ' - 1 = 2 , - 2 , - 2

Show! Vemos que ela realmente atravessa esse plano, com velocidade não nula :D

Passo 3

Agora, vejamos para o plano x O y . Neste caso, ela deve ter coordenada z = 0 na equação da posição. Para que isso aconteça, teremos:

t 2 + 1 = 0

t 2 = - 1

como isso é um absurdo, vemos que ela não atravessa esse plano ;) Assim, não temos também nenhuma velocidade para encontrar!

Passo 4

Finalmente, para o plano y O z , teremos que ter coordenada x = 0 para a posição. Isso acontece quando:

2 t = 0

t = 0

Quando t = 0 , a posição e velocidade da partícula são:

r 0 = 0 , - 1,1

r ' 0 = 2,0 , 0

Prontinho :D

Resposta

a) Passa pelo plano x O z nas posições 2,0 , 2 e - 2,0 , 2 , respectivamente com as velocidades 2,2 , 2 e 2 , - 2 , - 2 . Não passa pelo plano x O y . Passa pelo plano y O z na posição 0 , - 1,1 e com velocidade 2,0 , 0 .

Exercício Resolvido #4

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p.23. questão 11.

Dois carros se movem sobre pistas circulares concêntricas de raios 1km e 2km, respectivamente. O primeiro com velocidade angular constante de 20   r d / h . O segundo, parte do repouso, e mantem aceleração angular constante de 40   r d / h ² . Suponha que no instante inicial os dois carros estão emparelhados.

  1. Encontre os vetores posição para os dois movimentos
  2. Quanto tempo leva o segundo carro para se emparelhar novamente com o primeiro?
  3. Ache a velocidade do segundo carro neste instante.

Passo 1

a )

Os dois carros se movem ao longo de um circulo de mesmo centro e raios r 1 = 1 k m e r 2 = 2 k m . A parametrização do circunferência a gente já conhece:

x t = x 0 + r cos ⁡ t

y t = y 0 + r sen ⁡ t

t ∈ [ 0 ,   2 π ]

Lembrando: x 0 e y 0 são as coordenadas do centro das circunferências. Como o problema não deu esse dado, vamos considerá-las centradas na origem. Ou seja:

x 0 = y 0 = 0

Assim, seja σ 1 ( t ) o vetor posição do primeiro carro e σ 2 ( t ) o vetor posição do segundo carro, considerando x 0 = 0 e y 0 = 0 e substituindo os dados do problema, temos:

σ 1 θ 1 = 1 cos ⁡ θ 1 , 1 sen ⁡ θ 1 ,   θ 1 ∈ [ 0,2 π ]

E

σ 2 θ 2 = 2 cos ⁡ θ 2 , 2 sen ⁡ θ 2 ,   θ 2 ∈ [ 0,2 π ]

Eu chamei o t de θ porque esse parâmetro é, na verdade, um ângulo, mas como eu disse na teoria, quando a gente tá falando de vetor velocidade, temos que “transformar” o parâmetro em tempo.

Passo 2

Então a gente tem usar aquelas relações do movimento circular que te falei lá na teoria:

θ = θ 0 + θ ˙ t (movimento circular uniforme)

θ = θ 0 + θ ˙ 0 t + 1 2 θ ¨ t ² (movimento circular uniformentente variado)

O problema diz pra gente que o primeiro carro se move com velocidade angular contante de 20   r d / h , então:

θ 1 = θ ˙ 1 t + θ 0

θ 1 = 20 t + θ 0

E que o segundo, parte do repouso, e mantem aceleração angular constante de 40   r d / h ² , então:

θ 2 = θ 0 + θ ˙ 0 2 t + 1 2 θ ¨ 2 t 2

θ 2 = θ 0 + 0 t + 1 2 40 t 2

θ 2 = θ 0 + 20 t 2

Assim, os vetores posição são:

σ 1 θ 1 = 1 cos ⁡ θ 1 , 1 sen ⁡ θ 1

σ 1 t = 1 cos ⁡ 20 t + θ 0 , 1 sen ⁡ 20 t + θ 0

E

σ 2 θ 2 = 2 cos ⁡ θ 2 , 2 sen ⁡ θ 2

σ 2 t = 2 cos ⁡ θ 0 + 20 t 2 , 2 sen ⁡ θ 0 + 20 t 2

Passo 3

b )

O segundo carro se emparelha com o primeiro novamente quando as posições angulares dos dois carros forem iguais. Assim:

θ 1 = θ 2

20 t + θ 0 =   θ 0 + 20 t 2

20 t 2 - 20 t = 0

t ( 20 t - 20 ) = 0

t = 0

t = 1

O caso t = 0 não nos interessa pois é referente ao instante inicial em que já sabemos que os carros estão emparelhados.

Então, os carros voltam a se emparelhar quando t = 1   h o r a .

Passo 4

c )

Para encontrar o vetor velocidade do segundo carro temos que derivar o vetor posição do segundo carro e substituir em t = 1 :

σ 2 t = 2 cos ⁡ θ 0 + 20 t 2 , 2 sen ⁡ θ 0 + 20 t 2

σ ˙ 2 t = - 2 ( 40 t ) sen ⁡ θ 0 + 20 t 2 , 2 ( 40 t ) cos ⁡ θ 0 + 20 t 2

σ ˙ 2 t = - 80 t sen ⁡ θ 0 + 20 t 2 , 80 t cos ⁡ θ 0 + 20 t 2

Em t = 1 :

σ ˙ 2 t = - 80 ( 1 ) sen ⁡ θ 0 + 20 1 2 , 80 ( 1 ) cos ⁡ θ 0 + 20 ( 1 ) 2

Passo 5

A velocidade escalar do segundo carro é:

σ ˙ 2 = - 80 s e n θ 0 + 20 2 + 80 cos ⁡ θ 0 + 20 2

σ ˙ 2 = 6400 s e n 2 θ 0 + 20 + 6400 c o s 2 θ 0 + 20 = 80 k m / h

Resposta

  1. σ 1 t = 1 cos ⁡ 20 t + θ 0 , 1 sen ⁡ 20 t + θ 0 e

    2. σ 2 t = 2 cos ⁡ θ 0 + 20 t 2 , 2 sen ⁡ θ 0 + 20 t 2

  2. t = 1   h o r a
  3. 80 k m / h

Exercício Resolvido #5

George B. Thomas, Cálculo Volume II,11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pg. 257, exercício 3.

Encontre o vetor tangente unitário da curva

r t = t i + 2 3 t 3 2 k , t ∈ [ 0,8 ]

Passo 1

Temos que derivar o vetor r ( t ) para encontrar o vetor tangente e depois dividi-lo pelo seu modulo pra encontrar o vetor tangente unitário.

Passo 2

Derivando r ( t ) :

V t g → = r ' t = 1 i + t 1 2 k

Passo 3

Econtrando o módulo de V t g → :

V t g → = 1 2 + ( t 1 2 ) 2   = 1 + t

Passo 4

Encontrando o vetor tangente unitário:

T → = V t g → V t g → = 1 i + t 1 2 k 1 + t = 1 1 + t i + t 1 + t k

Resposta

T → = V t g → V t g → = 1 i + t 1 2 k 1 + t = 1 1 + t i + t 1 + t k

Exercício Resolvido #6

George B. Thomas, Cálculo Volume II,11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pg. 257, exercício 8.

Encontre o vetor tangente unitário da curva

r t = ( t s e n t + c o s t ) i + ( t c o s t - s e n t ) j , t ∈ [ 2 , 2 ]

Passo 1

Temos que derivar o vetor r ( t ) para encontrar o vetor tangente e depois dividi-lo pelo seu modulo pra encontrar o vetor tangente unitário.

Passo 2

Derivando r ( t ) :

V t g → = r ' t = ( s e n t + t c o s t - s e n t ) i + ( c o s t - t s e n t - cos ⁡ t ) j

V t g → = t c o s t i - t s e n t j

Passo 3

Econtrando o módulo de T → :

V t g → = ( t c o s t ) 2 + ( - t s e n t ) 2   = t ² = t = t pois t ∈ [ 2 , 2 ]

Passo 4

Encontrando o vetor tangente unitário:

T → = V t g → V t g → = t c o s t i - t s e n t j t =

cos ⁡ t i - s e n   t   j

Resposta

T → = V t g → V t g → = cos ⁡ t i - s e n   t   j

Exercício Resolvido #7

George B. Thomas, Cálculo Volume II,11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pg. 257, exercício 20.

Encontre o vetor tangente unitário para a involuta do circulo no ponto P ( x , y ) cuja parametrização é dada por:

x t = cos ⁡ t + t s e n   t

y t = s e n   t - t c o s   t

t > 0

Passo 1

Temos que derivar o vetor r t =   ( cos ⁡ t + t s e n   t , s e n   t - t c o s ) para encontrar o vetor tangente e depois dividi-lo pelo seu modulo pra encontrar o vetor tangente unitário.

Passo 2

Derivando r ( t ) :

V t g → = r ' t = ( - s e n t + t c o s t + s e n   t ,   c o s t + t s e n t - cos ⁡ t ) = ( t c o s t ,   t s e n t )

Passo 3

Econtrando o módulo de T → :

V t g → = ( t c o s t ) 2 + ( t s e n t ) 2   = t ² = t = t pois t > 0

Passo 4

Encontrando o vetor tangente unitário:

T → = V t g → V t g → = ( t c o s t ,   t s e n t ) t = ( c o s   t ,   s e n   t )

Resposta

T → = V t g → V t g → = ( c o s   t ,   s e n   t )

Exercícios de Livros Relacionados

(Regra da Cadeia). Sejam t → u t ,t ∈ I , u → F → u ∈ R n ,u ∈ J , funções deriváveis, onde I e J são intervalos em R . Suponha que, para todo t ∈ I , u t ∈ J . Prove que a função H → dada por H → t =
Calcule (d vec F)/(d t) e (d^2 vec F)/(d t^2) .vec F (t) = (3 t^2 , e^(- t) , ln ( t^2 + 1 ))
Suponha que μ p θ =c o s θ i - +s e n θj - , u θ θ =- s e n θi - + c o s θj - , r t = p t u p ( θ ( t ) ) , com θ = θ ( t ) e p = p ( t ) deriváveis até a segunda ordem no intervalo I . N o t a ç ã o
Determinar a derivada das seguintes funções vetoriais:d) f → t = e - t i → + e - 2 t j → + k →
Determinar a derivada das seguintes funções vetoriais:e) g → t = ln ⁡ t i → + tj → + tk →