Forma Quadrática – Quádricas
Produzido por Mariana PessanhaTeoria
Introdução
Pessoas! Como indica o título desse capítulo, a ideia é similar ao capítulo Forma Quadrática: Conicas, com uma pequena diferença, no caso, uma coordenada a mais!
Vamos relembrar rapidamente as quádricas que estudamos e suas equações:
- Elipsóide:
- Hiperbolóide de uma folha:
- Hiperbolóide de duas folhas:
- Cone Elíptico:
- Parabolóide Elíptico:
- Parabolóide Hiperbólico:
- Os termos lineares de , e indicam que a quádrica está deslocada em relação à origem.
- E os termos mistos , e indicam que a quádrica está rotacionada em relação aos eixos cartesianos.
Qualquer dúvida volte nos tipos sobre as quádricas
A ideia é aprender o que fazer quando aparece isso:
Já que essa equação não se encaixa em nenhuma das quádricas que estudamos. Na verdade, ela representa uma quádrica, cujo gráfico é uma superfície no . Portanto, seus pontos tem coordenadas , e .
O passo a passo pra resolução de problemas assim é essencialmente igual ao das cônicas. Você só vai ter que trabalhar com uma matriz , achar autovalores e autovetores.
Representação Matricial:
Como já dito, vimos 6 tipos de quádricas especiais. Porém quádrica é o conjunto de pontos que satisfazem a equação:
Bom, pegando novamente nossa equação lá em cima, reparem que:
É uma quádrica e pode ser escrita na forma matricial:
Para as quádricas, adicionamos uma coordenada naquela forma geral, então agora teremos:
E olha a matriz aí de novo!
Interpretação Geométrica
Bom, vamos voltar a equação na forma incial:
Temos duas observações importantes:
Como nossa quádrica está rotacionada e com o centro fora da origem, nós temos que encontrar os eixos nos quais a quádrica está , . Então vamos fazer todo aquele procedimento pra uma matriz .
Encontrando os eixos das quádricas rotacionadas
Tinhamos a equação de uma quádrica qualquer da forma:
Reescrevemos ela na forma matricial:
Para encontrar os eixos e , vamos reescrever a equação da quádrica utilizando os autovalores e autovetores da matriz .
A equação deverá ficar assim:
Aonde , e são os autovalores da matriz e ), e são os autovetores UNITÁRIOS associados à , e , respectivamente. Ou seja, a disposição dos autovetores na matriz deve acompanhar a dos autovalores.
Só pra relembrar, pra achar o UNITÁRIO de um vetor, basta dividir as coordenadas do vetor pelo seu MÓDULO!!!
Depois que você escrever a equação matricial, é só multiplicar as matrizes e encontrar a equação reescrita que a gente tava procurando nos eixos , e !!! YEAAAH!!
Exemplo
Vamos resolver aquele exemplo do início pra gente visualizar melhor:
Escrevemos na forma matricial:
A partir da matriz , encontramos seus autovalores , e e seus autovetores unitários associados , e .
Feito isso, podemos jogar os valores encontrados na equação matricial:
E então encontramos:
Multiplicando as matrizes, a gente chega em:
E assim como no exemplo das cônicas, vamos completar quadrados pra ver melhor nossa equação:
E dividindo toda a equação por , vamos chegar em:
Então, chegamos à conclusão de que aquela nossa equação “estranha” lá do início é, na verdade, um elipsoide no sistema de eixos , e . E esse elipsoide tem centro em e semieixos nas direções , e iguais a , e , respectivamente.
Lembre que assim como nas cônicas, as direções dos semieixos, e são dados pelas direções dos autovetores que nós encontramos da matriz .
E nessa hora, você provavelmente já estava pensando: SE ME PEDIREM PRA DESENHAR NO , EU CHORO!
Mas, porém, entretanto, todavia, fique tranquilo, pois NÃO vão te pedir pra desenhar no . Até porque convenhamos, nem os professores sabem desenhar direito no . Então, podem te pedir só as direções dos eixos , e , e aí é só mandar os autovetores e correr pro abraço!! “TOMA ESSA, PROVA DE CÁLCULO, SEGURA MEU GABARITO AEEE!!”
Bom, pessoal, é isso! Então vamos partir pros exercícios!
Encontrando os eixos das quádricas rotacionadas
Exercícios Resolvidos
Exercício Resolvido #1
Alfredo Steinbruch, Álgebra Linear, 2ª ed. São Paulo: Pearson Education do Brasil Ltda., pp 368 - 9
Identifique que a Quádrica na forma quadrática abaixo
Passo 1
Primeiramente, observamos que essa não é uma quádrica do jeito que estamos acostumados. Os termos elevados a potência 1 e os termos mistos nos levam a pensar que ela está com o centro deslocado e rotacionada.
Vamos escrever a sua equação na forma matricial:
Passo 2
A partir da matriz , encontramos seus autovalores.
Para calcular os autovalores de uma matriz 3x3:
Devemos fazer:
Isso implica:
No nosso caso:
Então temos:
Calculando:
Temos então:
Vamos procurar raízes através dos divisores tanto positivos quanto negativos do coeficiente do termo de menor grau dividido pelo coeficiente do termo de maior grau. Isso é:
Divisores de
São eles:
Vai dar trabalho, mas ao testar esses valores verificamos que as raízes são:
Passo 3
Precisamos encontrar os autovetores unitários.
Vamos calcular o autovetor referente a .Para isso faremos:
Temos:
Então:
Da primeira equação:
Substituindo na segunda:
Fica:
Arbitrando valores para temos:
Achando o autovetor unitário temos:
Passo 4
Calculando agora o autovetor referente a faremos:
Temos:
Então:
Da primeira equação:
Substituindo na segunda:
Fica:
Arbitrando valores para temos:
Achando o autovetor unitário temos:
Passo 5
Calculando agora o autovetor referente a faremos:
Temos:
Então:
Da primeira equação:
Substituindo na segunda:
Fica:
Arbitrando valores para temos:
Achando o autovetor unitário temos:
Passo 6
Agora que calculamos os autovalores e autovetores, podemos jogar os valores encontrados na equação matricial:
Fica:
Fazendo essa multiplicação matricial chegamos em:
Passo 7
Agora é só completar quadrados:
Substituindo na equação temos:
Ajeitando:
Que é a equação do elipsoide.
Resposta
A quádrica é um elipsoide.
Exercício Resolvido #2
Alfredo Steinbruch, Álgebra Linear, 2ª ed. São Paulo: Pearson Education do Brasil Ltda., pp 368 - 10
Identifique que a Quádrica na forma quadrática abaixo
Passo 1
Primeiramente, observamos que essa não é uma quádrica do jeito que estamos acostumados. Os termos de potência 1 e os produtos mistos nos levam a pensar que ela está com o centro deslocado e rotacionada.
Vamos escrever a sua equação na forma matricial:
Passo 2
A partir da matriz , encontramos seus autovalores.
Para calcular os autovalores de uma matriz 3x3:
Devemos fazer:
Isso implica:
No nosso caso:
Então temos:
Calculando:
Ajeitando:
Colocando em evidência:
Logo, os autovalores são:
Passo 3
Precisamos encontrar os autovetores unitários.
Vamos calcular o autovetor referente a .Para isso faremos:
Temos:
Então:
Multiplicando a primeira linha por 2 e somando com a terceira:
Temos:
Da primeira linha temos que:
E ? Não temos restrição nenhuma... Pode ser qualquer constantes.
Fica:
Arbitrando valores para temos:
Achando o autovetor unitário temos:
Passo 4
Calculando agora o autovetor referente a faremos:
Temos:
Então:
Da primeira equação:
Da segunda equação temos:
Fica:
Arbitrando valores para temos:
Achando o autovetor unitário temos:
Passo 5
Calculando agora o autovetor referente a faremos:
Temos:
Então:
Da primeira equação:
Da segunda:
Fica:
Arbitrando valores para temos:
Achando o autovetor unitário temos:
Passo 6
Agora que calculamos os autovalores e autovetores, podemos jogar os valores encontrados na equação matricial:
Fica:
Fazendo essa multiplicação matricial chegamos em:
Passo 7
Agora é só completar quadrados:
Substituindo na equação temos:
Ajeitando:
Que é a equação do hiperboloide de uma folha.
Resposta
Hiperboloide de uma folha.
Exercício Resolvido #3
Alfredo Steinbruch, Álgebra Linear, 2ª ed. São Paulo: Pearson Education do Brasil Ltda., pp 368 - 12
Identifique que a Quádrica na forma quadrática abaixo
Passo 1
Primeiramente, observamos que essa não é uma quádrica do jeito que estamos acostumados. Os termos de potência 1 e os produtos mistos nos levam a pensar que ela está com o centro deslocado e rotacionada.
Vamos escrever a sua equação na forma matricial:
Passo 2
A partir da matriz , encontramos seus autovalores.
Para calcular os autovalores de uma matriz 3x3:
Devemos fazer:
Isso implica:
No nosso caso:
Então temos:
Calculando o determinante caímos no polinômio característico:
Vamos tentar encontrar uma raiz testando os primeiros valores dos divisores de 162.
Por exemplo, vamos testar 2 e 3. Substituindo na equação verificamos que 3 é uma raiz. Portanto:
Agora vamos usar o método de briot-ruffini para diminuir um grau na equação. Funciona assim:
A primeira coisa a fazer é escrever essa equação completa, colocando vezes o elevado aos graus que não aparecem (já está nessa forma):
Agora montamos o seguinte quadrinho:

No canto superior esquerdo colocamos os coeficientes da nossa equação, no canto superior direito colocamos o valor na nossa raiz .
Agora nós fazemos os seguintes passos. Primeiro descemos o primeiro coeficiente, que vai ficar:

O próximo passo é multiplicar esse número que baixamos pelo número ali no canto superior direito, e depois somar com o próximo coeficiente.
Nesse caso fazemos
Esse nessa equação imediatamente acima é o coeficiente, o 3 é o número do canto superior direito e aquele outro é o próximo coeficiente.
Fazendo essa conta chegamos ao valor , colocamos esse valor embaixo do coeficiente , ficando:

Agora é só repetir, a nossa conta dessa vez vai ficar:
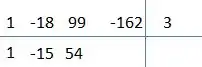
Agora é só repetir, a nossa conta dessa vez vai ficar:

Como aquele último cara deu a nossa conta está certinha, se não der alguma conta está errada.
A nossa nova equação vai ser aquela que tem os coeficientes de baixo, tirando aquele , começando com um grau a menos do que o anterior, neste caso vamos ter:
Resolvendo encontramos:
Então temos:
Passo 3
Precisamos encontrar os autovetores unitários.
Vamos calcular o autovetor referente a . Para isso faremos:
Temos:
Então:
Da primeira equação:
Da terceira equação temos:
Fica:
Arbitrando valores para temos:
Achando o autovetor unitário temos:
Passo 4
Calculando agora o autovetor referente a faremos:
Temos:
Então:
Da primeira equação:
Da terceira equação:
Fica:
Arbitrando valores para temos:
Achando o autovetor unitário temos:
Passo 5
Calculando agora o autovetor referente a faremos:
Temos:
Então:
Da primeira equação:
Da terceira:
Fica:
Arbitrando valores para temos:
Achando o autovetor unitário temos:
Passo 6
Agora que calculamos os autovalores e autovetores, podemos jogar os valores encontrados na equação matricial:
Fica:
Fazendo essa multiplicação matricial chegamos em:
Que é a equação de um elipsoide.
Resposta
A quádrica é um elipsoide.