Introdução às Curvas e Domínio de Curvas
Teoria
Introdução
Aqui vamos entender um pouquinho melhor como vemos matematicamente uma curva.
Vamos pegar os vetores
Vamos ver como fica graficamente esses caras
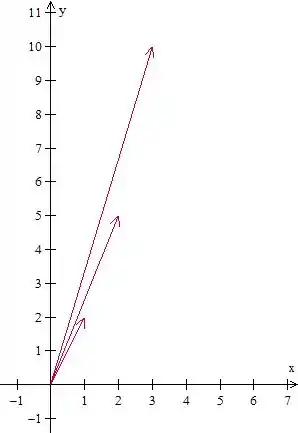
Olhando assim isso faz sentido nenhum né? Três setas aleatórias? Vou pintar uma bolinha no final de cada uma
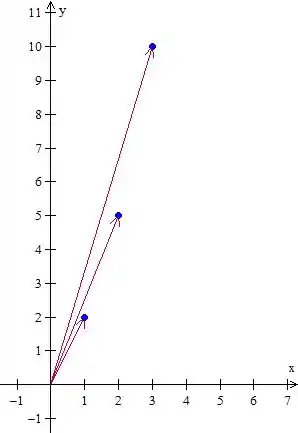
Se pensarmos só nessas bolinhas azuis, isso pode ser visto como a posição de algum objeto por exemplo.
Se pegarmos mais vetores que apontam para as posições que esse objeto passou vamos ter algo mais ou menos assim
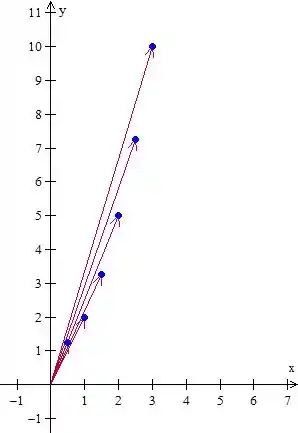
Essas setas não ajudam em nada né? Vamos olhar só para os pontinhos azuis
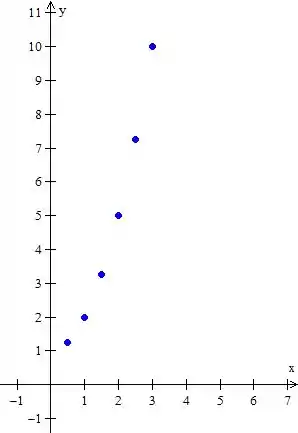
Opa, repara que isso parece o caminho que o objeto fez. Se pegarmos uma quantidade bizarramente gigante de pontos podemos ver bem esse caminho.
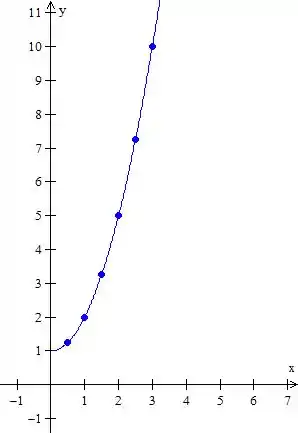
Repara que cada ponto desse tem um vetor. Podemos ter em cada um deles funções que dependem do tempo por exemplo
Escrever uma curva matematicamente nada mais é que achar essa função que nos dá os vetores que indicam a posição de um objeto.
Seria algo assim
Se estivéssemos em seria igual, mas com o também
Vamos entender um pouco melhor disso, essa função representa a curva, mas ela tem um nome especial: Parametrização da Curva.
E essas funções , e são as equações paramétricas da curva. Muitas vezes nos referimos a elas como as componentes da parametrização!
OBS: Esse parâmetro pode ser qualquer coisa, ,, não importa. Em cada caso ele pode ter um significado e uma lógica, mas é tudo parametrização de uma curva porque temos apenas UM parâmetro blz? Nenhuma outra letra aparece só esse , ou que aparece na questão
Intervalo da Parametrização da Curva
Se eu só te falar a curva é
Isso não vai ser o suficiente, preciso te dizer também como funciona esse .
Nesse caso o nosso pode variar de qualquer forma, não vai ter problema de número em nenhum deles. Mas definir esse intervalo direito diz exatamente como é essa curva. Fique atento a isso.
Mas se liga nessa função
Aqui o pode valer qualquer coisa? Tem aquela raiz atrapalhando nossa vida ali. Se não definirmos esse intervalo a coisa pode ficar feia, imagina aparecer um número complexo junto com cálculo para atazanar a nossa vida.
Então sempre colocamos esse intervalo junto, fica assim, por exemplo
Na questão de prova ele pode te pedir esse intervalo , normalmente nessa situação ele chama de Domínio. WTF man!!! Não faz isso comigo... Dá aquela vontade de chorar, mas se acalme.
O domínio nada mais é que o intervalo que as funções das componentes estão definidas. Não tem nenhum denominador dando zero na parada, raízes quadradas negativas, logaritmos negativos, sacou?
Vamos ver um exemplo
Pela primeira componente precisamos ter
E pela segunda
Nesse caso qual o domínio de ? Precisamos obedecer todos os dois, então vai ser
Só isso, partiu exercícios?
Intervalo da Parametrização da Curva
Exercícios Resolvidos
Exercício Resolvido #1
Hamilton Luiz Guidorizzi, Um curso de cálculo Volume II, 5ª ed. Rio de Janeiro: LTC, 2001, pg.121, exercício 3 - modificado
Determine o domínio
Passo 1
a)
Para achar o domínio temos que ver as restrições que a nossa função tem. Para isso vamos olhar a restrição de cada componente e juntar tudo no final.
Passo 2
A primeira componente é então não temos problemas. A segunda componente é uma fração dentro da raiz. Então precisamos ter
Repara que o numerador é positivo, então precisamos ter
Fica atento que eu não coloquei maior ou igual, porque o denominador não pode ser zero!!
Passo 3
Vamos ver agora a terceira componente. Nela precisamos que o cara dentro do seja positivo.
Esse cara é uma função de grau, com o coeficiente de negativo. Então ele é positivo entre as raízes.
Então temos
Passo 4
Precisamos agora juntar esses intervalos, afinal eles precisam valer todos ao mesmo tempo
Então o resultado final vai ser