Parametrizações com Geometria
Produzido por Mariana PessanhaTeoria
Ferramentas
O que nos interessa aqui é parametrizar curvas cuja parametrização a gente não conhece de cara. Para isso, algumas ferramentas são úteis, como a parametrização da circunferência, da reta, da elipse e etc.
Mas antes, eu preciso te lembrar de alguns conceitos tranquilinhos de geometria analítica. Vamos lá:
- Ponto médio: ponto médio de um segmento é aquele que divide o segmento em duas partes iguais. Suas coordenadas são:
- Equação da reta: seja uma reta não-vertical, com coeficiente angular , que passa pelos pontos e .
- Interseção entre figuras: quando duas curvas se intersectam num ponto, temos que esse ponto pertence a essas duas figuras, assim, deve satisfazer as equações de ambos.
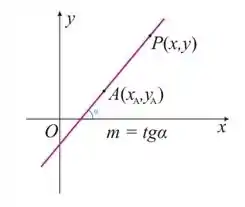
O coeficiente angular dessa reta é dado por:
Assim, a equação da reta é:
Por exemplo, se a gente quiser saber em quais pontos a circunferência e a reta se intersectam, vamos ter que pensar nessa parada aí que acabei de falar.
Temos
Substituindo na equação da circunferência, temos:
Resolvendo essa equação do segundo grau, encontramos que:
Assim, como :
Para :
Para :
Logo, os pontos em que as figuras se intersectam são e .
Tranquilo, favorável?
Como você viu, não tem muita teoria. Então bora praticar com os exercícios pois eles são fundamentais para concretizar seu conhecimento.
Exercícios Resolvidos
Exercício Resolvido #1
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p.12. questão 4.
Uma haste, presa na origem do plano , ocupa a posição da reta . A haste intercepta a reta no ponto e a elipse no ponto (figura). Quando varia, o vértice do triângulo descreve uma curva.
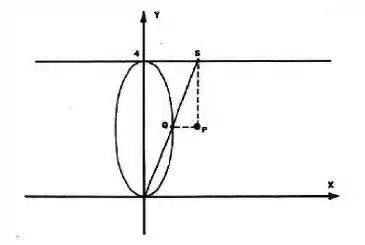
Escreva as equações paramétricas dessa curva em função do parâmetro .
Passo 1
Vamos lá, as coordenadas do ponto são:
O que a gente precisa é encontrar uma relação entre as coordenadas desse ponto e as coordenadas e dos pontos e .
Observando a figura a gente percebe que:
Assim
Passo 2
Agora vamos encontrar as coordenadas dos pontos e .
Comecemos pelo ponto .
O que sabemos dele? Sabemos que sua coordenada é sempre constante e igual ! Assim,
Agora, sabemos também que o ponto pertence à reta então:
Logo:
Passo 3
Para saber as coordenados do ponto , usamos o fato de que pertence a reta e a elipse . Assim, a coordenada do ponto é igual a :
Se substituirmos isso na equação da elipse, encontramos a coordenada do ponto Q
O caso não nos interessa pois representa a origem e nosso ponto não está na origem. Logo, as coordenadas do ponto Qsão:
Passo 4
Voltando agora para aquela relação que encontramos lá no incio.
Temos então que:
Resposta
Exercício Resolvido #2
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p.13. questão 6.
A involuta de uma circunferência é a curva traçada pelo ponto de extremidade de um fio quando o mesmo, mantido tenso, é desenrolado de um carretel fixo (figura). Supondo que o centro do carretel está colocado na origem do plano e seu raio é , e que o fio começa a se desenrolar no ponto . Mostre que as equações paramétricas da Involuta, ao desenrolar uma volta do fio no carretel são:
e ,
Utilizando como parâmetro o ângulo mostrado na figura.
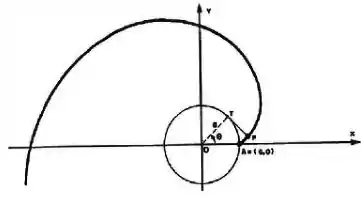
Passo 1
Para descobrirmos a parametrização da involuta, temos que achar o vetor posição do ponto .
Podemos pensar esse vetor como a soma dos vetores e
Sabemos que:
Repare que nada mais é que o arco esticado, então:
(comprimento do arco )
Passo 2
Beleza, agora podemos achar também um vetor tangente ao vetor :
Esse vetor é paralelo ao vetor , mas está no sentido oposto a ele. Vamos utilizar essas informações por partes.
Como está no sentido oposto de e , devemos inverter o sentido de :
(sentido invertido)
Como já sabemos que é paralelo a e a informação que temos sobre é a respeito de seu comprimento, vamos achar o comprimento de :
(porque
Opa, o comprimento de e diferem por um fator multiplicativo Então, para e virarem o mesmo vetor, temos que multiplicar por (para que os comprimentos dos dois vetores fiquem iguais, agora que eles já tem o mesmo sentido):
Passo 3
Agora, como sabemos que
Substituindo os resultados encontrados, temos:
,
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
UFRJ, Cálculo Diferencial e Integral 2, P1 2015.1, questão 2
A reta que passa pela origem e faz ângulo com o eixo , intercepta a circunferência no ponto . Seja o ponto médio do segmento na figura abaixo. Determine as coordenadas de em função do ângulo . Perceba que, quando varia entre e , o ponto percorre a curva da figura.
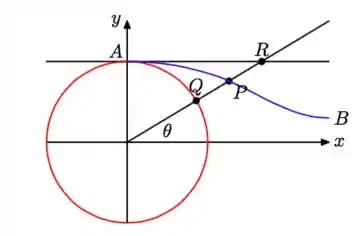
Passo 1
Vamos lá! é o ponto médio do segmento , certo? Então, se as coordenadas de e são, respectivamente, e , as coordenadas do ponto são:
Beleza até agora?
Passo 2
Assim, tudo o que temos que fazer é encontrar cada uma dessas coordenadas! Comecemos pelo ponto ...
O que sabemos dele? Sabemos que pertence sempre à circunferência de raio ! Assim, podemos dizer que suas coordenadas estão no modelo:
Ok, e sobre o ponto , o que sabemos dele? Sabemos que sua coordenada é sempre constante e igual ao raio da circunferência! Assim,
E ainda podemos descobrir a relação que tem com e . Veja que no triângulo de vértices , e , temos que:
E, assim,
E o ponto pode ser descrito por:
Passo 3
Colocando esses valores para e na equação de , teremos:
Prontinho, aí está o nosso ponto !
Resposta
O ponto é