Esboço de Curvas
Teoria
Equação cartesiana
Imagine que queremos esboçar o gráfico da curva:
E aí? O que a gente faz? Bom, a primeira coisa a se fazer é encontrar a equação cartesiana da curva.
Uma equação cartesiana de uma curva é aquela em que não aparece o parâmetro , apenas as variáveis e .
É o caminho inverso ao que estamos fazendo até agora, quando desejamos parametrizar uma curva. Nesse caso, teríamos uma curva parametrizada e gostaríamos de saber qual é a equação cartesiana dela.
Temos o seguinte:
Isolamos na primeira equação:
E substituímos na outra equação:
Portanto, temos que essa curva é uma parábola.
Equação cartesiana: funções trigonométricas
Agora, imagine que um problema pede para esboçar essa curva:
O ponto chave aqui é como encontrar a equação cartesiana. Basicamente, você vai analisar cada componente da curva e tentar relacioná-los.
Agora pensa comigo, na nossa curva, a gente tem seno e cosseno. O que que dá pra fazer com isso? O que isso pode dizer pra gente sobre a curva?
Lembra da relação fundamental da trigonometria? Não? Relaxa que eu te lembro:
Então, parece que ela pode nos ajudar né? E pode mesmo!! Repara que para qualquer , temos que:
Ou seja, os pontos estão sempre sobre um círculo de raio . E a coordenada , por sua vez, cresce indefinidamente. Então, o esboço da curva fica:
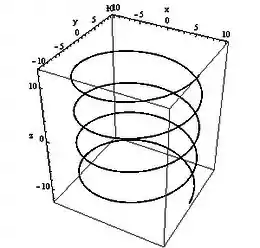
Que curva é essa? É uma curva helicoidal cilíndrica. Repare ainda que , portanto a curva está “subindo” ao longo do eixo .
Algumas variações
Observação 1: Da mesma forma, os pontos poderiam estar sobre uma elipse, em vez de estar sobre uma circunferência. Por exemplo:
Vamos fazer o seguinte:
Ou seja, os pontos estão sobre essa elipse. Tranquilo?
Observação 2: Vamos ver o que fazer quando for uma função qualquer de . Por exemplo:
Nesse caso, a única diferença é que o eixo cresce mais rápido por ser uma exponencial.
Observação 3:
Observe que para todo . Ou seja, a curva estará em cima da superfície do cone . Seu esboço fica:
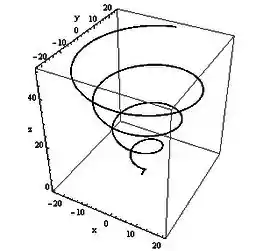
Que é uma curva helicoidal cônica.
Em resumo:
Caso o problema peça para você fazer um esboço da curva, será uma dessas duas.
- Se - curva helicoidal cilíndrica
- Se - curva helicoidal cônica
Tenha essas duas curvas em mente. Elas podem aparecer na prova! E, caso seja necessário, você saberá desenhá-las. Mas não se preocupe, não precisa ser nada muito perfeccionista. Apenas observe o ponto inicial da curva, o sentido que ela percorre à medida que aumenta e o intervalo em que está contido.
Só mais uma dica
O problema é que às vezes vamos ter que esboçar curvas difíceis de identificar!
Nesse caso o jeito é fazer o basicão: substituir vários valores de na parametrização e assim achar pontos da curva.
Exemplo: Vamos esboçar a curva parametrizada por .
É muito difícil de identificar de cara que curva é essa! Tem um cosseno e um seno, beleza, mas e aí? É justamente nesse caso que partimos pro trabalho braçal de substituir vários pontos e ver no que dá.
Então vamos lá! É bom pegar o máximo de valores possíveis pra ter mais pontos.
De até podemos ver que vamos ter os mesmos valores, mas com o sinal trocado:
Pronto! Vamos ver como ficaram esses pontos bonitões:
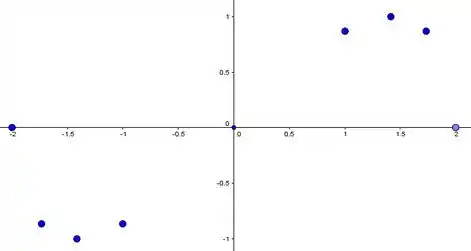
Dá pra ter uma noção boa de como é a curva né?
Só ali perto da origem ( que não tem muitos pontos... Aí daria pra ver com mais calma como ficam e perto de . Na dúvida faz uma reta mesmo!
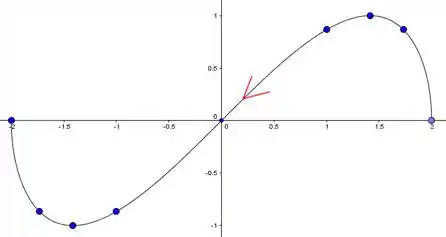
Saca só como fica a curva:
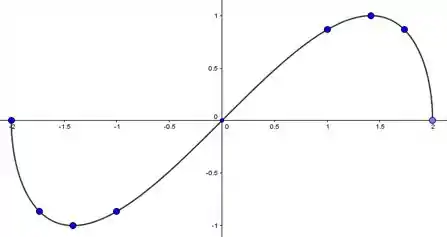
E se a questão pedir pra indicar a orientação, basta botar uma seta pra esquerda! Né? Fomos de , que corresponde ao ponto lá na direita, até , no ponto .
Então o esboço ficaria assim:
Belezinha? Então vem comigo treinar nos exercícios!
Equação cartesiana: funções trigonométricas
Algumas variações
Só mais uma dica
Exercícios Resolvidos
Exercício Resolvido #1
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p.11. questão 1, itens a,c,f.
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine sua equação cartesiana:
a) , ,
c) , ,
f) , ,
Passo 1
Podemos isolar o parâmetro na primeira equação e substituir na segunda, assim:
Temos a reta
Passo 2
Verificar intervalo para a curva da letra a:
não tem nenhuma limitação. Assim, .
Passo 3
Avaliar o sentido percorrido na curva da letra a: nós temos que ver se a derivada vai ser positiva ou negativa. Positiva, a função está crescendo. Negativa, a função está decrescendo.
Podemos observar que
Logo, a curva está “descendo”.
Passo 4
Esboçar a curva da letra a:
Como é real, ele varia de a e, nesse caso, nossa reta não tem nenhuma limitação. Quando , a curva passa pelo ponto que eu marquei ai.
Passo 5
Na letra c, vamos usar a relação fundamental da trigonometria
Assim, observamos que
Logo, também temos a reta .
Passo 6
Verificar o intervalo para a curva da letra c:
é uma função limitada, está sempre entre 0 e 1. Assim, e .
Passo 7
Avaliar o sentido percorrido pela curva da letra c:
Podemos observar que
Mas
Logo
E nesse intervalo, tanto o seno como o cosseno são positivos, então
Como o ponto inicial, ou seja, em vai ser
A curva começa em e o valor de vai aumentar.
Então ela está “subindo”.
Passo 8
Esboçar a curva da letra c
Passo 9
Na letra f pelo enunciado temos
E ele deu que
Então queremos achar uma relação de e
Lembrando das relações trigonométricas
E
Podemos usá-las para achar a função de e
Mas
Então
Temos a parábola
Passo 10
Avaliar o intervalo para a curva da letra f:
Vamos começar olhando o valor de
O seno indo de a , nos diz que o valor de vai de à .
Assim,
Passo 11
Vamos olhar o agora
Se
Então
Isso nós diz que o vai de à
Passo 12
A nossa curva vai ser
Passo 13
Vamos avaliar como varia essa função.
Como
Então
Isso nós diz que
Assim
E o valor de vai estar diminuindo.
A curva vai começar em
Então ela está “descendo”
Resposta
a)
c)
f)
Exercício Resolvido #2
Elaboração Própria
Seja a curva parametrizada:
Faça um esboço da trajetória percorrida pela partícula.
Passo 1
Identificar curva:
Pelas equações paramétricas da curva, podemos ver que
Como , então essa é uma helicoidal cilíndrica.
Passo 2
Avaliar :
Logo, a curva “sobe” com o aumento do parâmetro
Passo 3
Verificar intervalo e ponto inicial:
Vamos calcular o ponto da trajetória correspondente a
Passo 4
Esboçar curva:
Só uma observação: vimos que a curva tem que começar no ponto e na imagem ela está começando na altura . Isso porque é difícil de definir o ponto inicial da curva no programa que a gente usa pra fazer esses gráficos 3D. Enfim, só ficar atento nessa questão do ponto inicial ;)
Resposta
Obs: início no ponto
Exercício Resolvido #3
Elaboração Própria
Seja a curva parametrizada:
Faça um esboço da trajetória percorrida pela partícula.
Passo 1
Identificar curva:
Pelas equações paramétricas da curva, podemos ver que
Logo:
Então essa é uma helicoidal cônica.
Passo 2
Avaliar :
Logo, a curva “sobe” com o aumento do parâmetro
Passo 3
Verificar intervalo e ponto inicial:
Como t é real, ele varia de a . Quando , a curva passa pelo ponto:
Passo 4
Esboçar curva:
Resposta
Exercício Resolvido #4
USP, Cálculo 2, P1, 2012.2, questão 1a
Esboce a imagem da curva dada por
Passo 1
Numa parametrização, cada coordenada corresponde a uma dimensão da função no plano cartesiano. A primeira coordenada corresponde à componente , a segunda à componente , a terceira à e assim por diante.
Então, podemos dizer que, a para a curva dada:
Passo 2
Na equação de cima, podemos colocar o em evidência no lado direito, e teremos:
Mas . Então, teremos que:
E ainda temos como simplificar isso! Perceba, quando tivermos algo ao quadrado, e do lado duas vezes esse algo, podemos completar quadrados somando e subtraindo o mesmo número. Fica assim:
E perceba que o termos entre parêntesis vale :
E, por fim, sabemos que . Assim, temos que:
Ou seja, a parte de cima do sistema é , e ele fica:
Passo 3
Legal, agora que temos o em função do , sabemos que a parametrização está sobre a parábola .
Mas e quanto ao ? Ele está em função de , e essa é uma função limitada (ela nunca é menor que e nem maior que ). Então, a expressão para o , dada por:
sempre vai estar entre e , pois, como disse, está entre e (basta subtrair do maior e menor valor assumido por )
Passo 4
Pronto!! Agora sabemos que , e que varia entre e . Logo, a imagem da nossa curva parametrizada é o pedaço da parábola no qual os valores de estão entre e
A parábola deitada é e a faixa são os valores de . A interseção desses dois lugares, é parte da parábola que está dentro da faixa!
Resposta
Parte da parábola dentro da faixa:
