Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Vetor Normal

Ver Todos os Exercícios

Teoria

Opaa, seja bem vindo ao Responde Aí! Bora bater um papo sobre vetor normal?!

O que é um Vetor Normal?

O vetor normal é o vetor perpendicular ao vetor tangente! Assim:

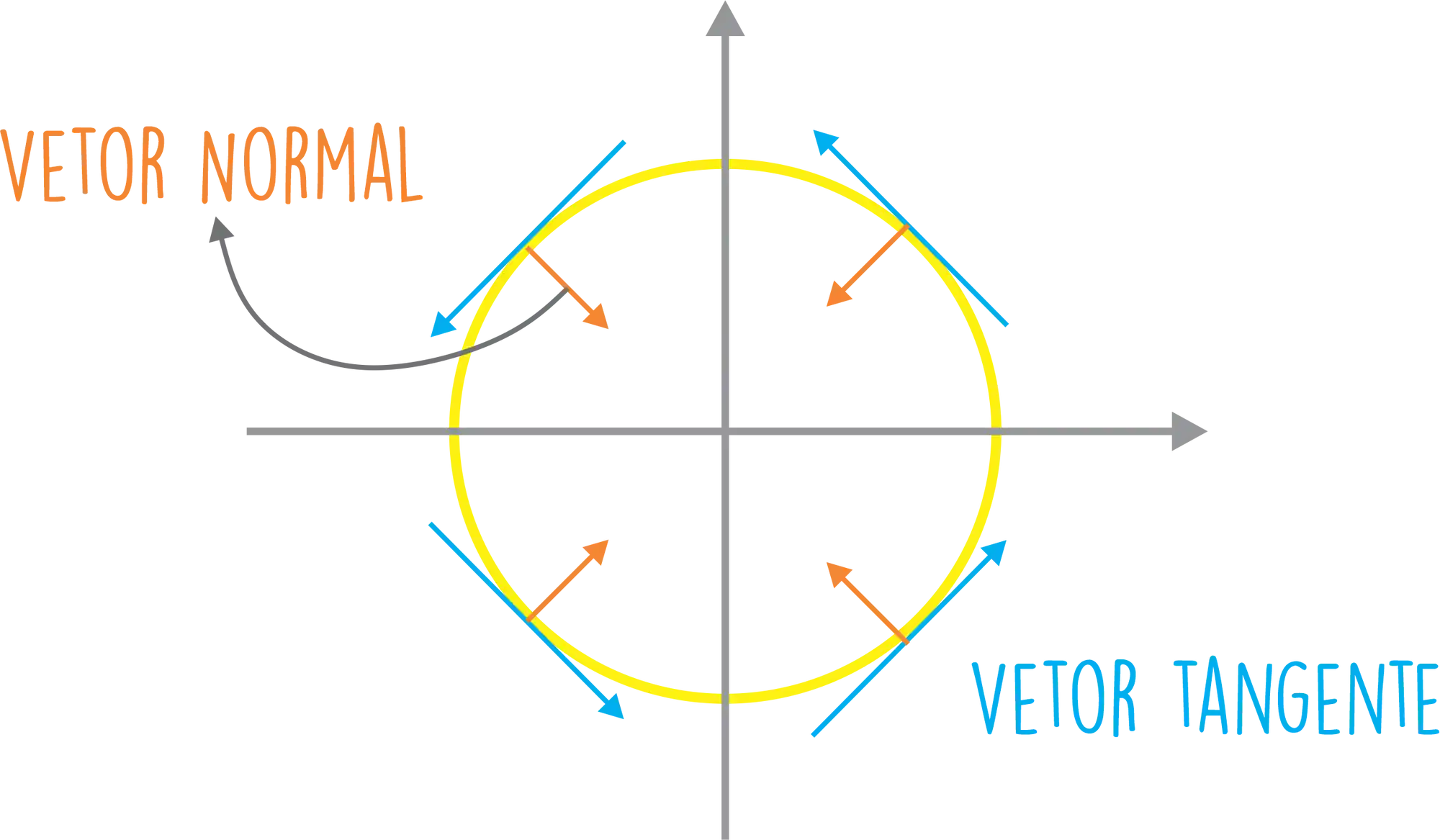
Vetor normal
Vetor normal

Lembra que o vetor tangente? É aquele toca a curva em um determinado ponto, sua direção indica o movimento desse vetor! Ou seja, o vetor normal é perpendicular ao movimento 🤩

Hoje a gente vai aprender como calcular o vetor normal à um plano, para isso a gente vai usar a equação parametrizada. Que tem essa carinha aqui:

Se você ainda fica meio confuso com parametrização, dá uma conferida aqui 👇👇👇

Como Calcular um Vetor normal a um Plano

Para calcular o vetor normal, usamos a seguinte fórmula:

separar

Onde é a derivada do vetor tangente e é o seu módulo. Bora fazer um exemplo?

Você também pode conferir esse conteúdo em vídeo:

Passo 1: Achar o vetor tangente Unitário

A primeira coisa que temos que fazer é encontrar o vetor tangente, e a gente faz isso derivando :

Para saber o vetor tangente unitário, nós temos que dividir pelo módulo. Então vamos calcular o módulo:

Agora é só dividir:

Passo 2: Derivar o vetor tangente Unitário e achar seu módulo

Derivamos o vetor tangente:

Calculamos o seu módulo:

Passo 3: Substituir na fórmula e achar o vetor normal

Lembra da fórmula de vetor normal?!

Substituímos suas variáveis:

Prontinhoo! Agora vamos praticar com exercícios?

Exercícios Resolvidos

Exercício Resolvido #1

George B. Thomas, Cálculo,Volume II,11º ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pg. 263, exercício 1.

Encontre o vetor normal para a curva plana

r t = t   i + ln ⁡ c o s t   j ,   - π 2 ≤ t < π 2

Passo 1

Bom, a primeira coisa que temos que fazer é encontrar o vetor tangente:

v t → = r ' ( t ) = 1 ,   - s e n   t cos ⁡ t = ( 1 , - t g   t )

v t → = 1 2 + - t g   t 2 = 1 + t g ² t = s e c ² t = | sec ⁡ t |

Como - π 2 ≤ t < π 2 , temos que sec ⁡ t > 0 , portanto podemos desprezar o módulo

v → t = sec ⁡ t

Passo 2

Dividir o vetor tangente pelo seu módulo para encontrar o vetor tangente unitário:

T → t = v t → v t → = ( 1 , - t g   t ) sec ⁡ t = 1 sec ⁡ t , - t g   t sec ⁡ t = ( cos ⁡ t ,   - s e n   t )  

Passo 3

Agora derivamos o vetor tangente unitário:

T → ' t = ( - s e n   t ,   - cos ⁡ t )

E calculamos seu módulo:

T → ' t = - s e n   t 2 + - cos ⁡ t 2 = s e n 2 t + c o s 2 t = 1

Passo 4

Fim da questão: é só substituir na fórmula:

N → = T → ' t T → ' t

N → = ( - s e n   t ,   - cos ⁡ t ) 1 = ( - s e n   t ,   - cos ⁡ t )

Resposta

N → = ( - s e n   t ,   - cos ⁡ t )

Exercício Resolvido #2

George B. Thomas, Cálculo,Volume II,11º ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pg. 263, exercício 14.

Encontre o vetor normal para a curva

r t = c o s 3 t   i + s e n 3 t   j ,   0 ≤ t ≤ π 2

Passo 1

Bom, a primeira coisa que temos que fazer é encontrar o vetor tangente:

v t → = r ' ( t ) = 3 ( - s e n   t ) c o s ² t ,   3 cos ⁡ t s e n ² t = ( - 3 s e n ( t ) c o s ² ( t ) , 3 c o s ⁡ ( t ) s e n ² ( t ) )

v t → = - 3 s e n ( t ) c o s ² ( t ) 2 + 3 cos ⁡ t s e n 2 t 2 = 9 s e n 2 t c o s 4 t + 9 c o s 2 t s e n 4 t

v t → = 9 c o s ² t s e n ² t ( c o s 2 t + s e n 2 t ) = | 3 c o s ⁡ ( t ) s e n ( t ) |

Como 0 ≤ t < π 2 , cos ⁡ t e sin ⁡ t são maiores que zero, então podemos esquecer o módulo

v → t = 3 cos ⁡ t sen ⁡ t

Passo 2

Dividir o vetor tangente pelo seu módulo para encontrar o vetor tangente unitário:

T → t = v t → v t → = ( - 3 s e n ( t ) c o s ² ( t ) , 3 c o s ⁡ ( t ) s e n ² ( t ) ) 3 c o s ⁡ ( t ) s e n ( t ) = - cos ⁡ t , s e n   t

Passo 3

Agora derivamos o vetor tangente unitário:

T → ' t = ( s e n   t ,   cos ⁡ t )

E calculamos seu módulo:

T → ' t = s e n   t 2 + cos ⁡ t 2 = s e n 2 t + c o s 2 t = 1

Passo 4

Fim da questão: é só substituir na fórmula:

N → = T → ' t T → ' t

N → = ( s e n   t ,   cos ⁡ t ) 1 = ( s e n   t ,   cos ⁡ t )

Resposta

N → = ( s e n   t ,   cos ⁡ t )

Exercício Resolvido #3

George B. Thomas, Cálculo,Volume II,11º ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pg. 263, exercício 7.

  1. Mostre que n t = - g ' t i + f ' t j e - n t = g ' t i - f ' t j são ambas normais à curva r t = f t i + g t j no ponto ( f t , g t ) .

    2. Para obter N → para uma curva plana em particular, podemos escolher n → e - n → do item (a) que aponta para o lado côncavo da curva e torna-lo um vetor unitário. Aplique esse método para encontrar N → para as curvas a seguir:

  2. r t = t   i + e 2 t   j  
  3. r t = 4 - t 2   i + t   j   ,   - 2 ≤ t ≤ 2

Passo 1

Para demonstrar o que ele quer, podemos pensar assim: pela curva, podemos obter o vetor tangente. Se esse vetor for normal a curva o produto escalar deve ser zero!

Passo 2

A primeira coisa que fazemos é encontrar o vetor tangente:

v t → = r ' t = f ' t , g ' t

Agora vamos calcular o produto escalar

n t ⋅ v t → = - g ' t i + f ' t j ⋅ f ' t i + g ' t j = - g ' t f ' t + f ' t g ' t = 0

Beleza, agora a gente sabe que n ( t ) é realmente normal a curva.

Passo 3

Agora para - n ( t ) observa só uma coisa:

- n t ⋅ v t → = - n t ⋅ v t → = - 0 = 0

Ou seja, esse produto escalar também dá zero! Então, - n ( t ) também é normal a curva.

Passo 4

Nas letras b e c vamos escolher n t = - g ' t i + f ' t j . Temos:

b ) f t = t e g t = e 2 t → f ' t = 1 e g ' t = 2 e 2 t

Logo,

n t = - 2 e 2 t i + 1 j

c )   f t = 4 - t 2   e g t = t → f ' t = - t 4 - t 2   e g ' t = 1

Logo,

n t = - 1 i - t 4 - t 2 j

Passo 5

Agora, precisamos torna-los vetores unitários:

b )   n t = - 2 e 2 t 2 + 1 2 = 4 e 4 t + 1

N → = n t n t = - 2 e 2 t i + 1 j 4 e 4 t + 1 = - 2 e 2 t i 4 e 4 t + 1 + 1 j 4 e 4 t + 1

c )   n t = - 1 2 + - t 4 - t 2 2 = 1 + t 2 4 - t 2 = 2 4 - t 2

N → = n t n t = - 1 i - t 4 - t 2 j 2 4 - t 2 = - 1 2 ( 4 - t 2 i + t   j )

Resposta

b ) N → = - 2 e 2 t i 4 e 4 t + 1 + 1 j 4 e 4 t + 1

c ) N → = - 1 2 ( 4 - t 2 i + t   j )

Exercícios de Livros Relacionados

Atalho eventual para curvatura - Se você já conhece a N e v , então a fórmula a N = κ v 2 fornece uma maneira conveniente de encontrar a curvatura. Utilize-a para encontrar a curvatura e o raio de cur
Mostre que uma partícula em movimento irá se mover em uma linha reta se o componente normal de sua aceleração for zero.
Curvatura totalEncontramos a curvatura total da parte de uma curva suave que vai de s = s0 a s = s1s0 integrando κ de s0 a s1. Se a curva possui outro parâmetro, digamos t, então a curvatura total é K
Encontre uma equação para o círculo de curvatura da curva r(t) = ti + (sen t)j no ponto (π/2, 1). (A curva parametriza o gráfico de y = sen x no plano xy).
Encontre uma equação para o círculo de curvatura da curva r(t) = (2 ln t)i – [t + (1/t)]j, e - 2 ≤ t ≤ e 2 , no ponto (0, –2), em que t = 1.